Вращение молекулы

Введение.

Микроволновая спектроскопия является одним их трех главных методов исследования геометрии молекул. А геометрическое строение свободных молекул имеет особое значение для химии, так как составляет основу теории химического строения молекул.

В этом курсе мы остановимся только на методе микроволновой спектроскопии хотя бы потому, что этим методом в свое время занимались в ИНФОУ Кроме того, применение этих методов ограничивается исследованием только сравнительно малых молекул, поэтому для общего представления об их возможностях достаточно будет ознакомления с одним из них. Два других метода оставляются для самостоятельного ознакомления заинтересованных лиц. Один из них основан на получении чисто вращательных спектров комбинационного рассеивания и менее распространен, чем микроволновая спектроскопия, другой метод – метод газовой электронографии – относится к дифракционным методам.

9.2.1. Оси вращения, направление вращения.

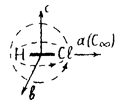
Вращение молекулы можно разложить по трем взаимно перпендикулярнвм координатам (осям а, b и с), как это показано на рисунке:

Моменты инерции І:

І_а – вокруг связи (ось а), I_b – в плоскости листа (ось b), І_с – перпендикулярно плоскости бумаги (ось с).

9.2.2. Типы вращающихся молекул.

9.2.2.1. Линейные молекулы H-Cl, O=C=S (I_a = 0, I_b = I_c).

9.2.2.2. Симметричный волчок СН₃-F: I_a ¹ 0, I_b = I_c ¹ I_a

9.2.2.3. Сферический волчок: СН₄ (I_a = I_b = I_c).

9.2.2.4. Асимметричный волчок: О Н Н

(I_a ¹ I_b ¹ I_c). Н Н, С = С

Н Cl

9.3. Двухатомная молекула (I_a = 0, I_b = I_c).

3.1. Модель двухатомного жесткого ротатора.

Это наиболее простая модель, в которой длина связи не меняется при вращении, а атомы не совершают колебательных движений. Параметры этой модели:

m₁ O m₂ r_o = r₁ + r₂ , O – центр тяжести, где в условиях равнове-

сия m₁r₁ = m₂r₂, момент инерции I = m₁r₁² + m₂r₂² =

= m₁r₁r₂ + m₂r₂r₁ = r₁r₂(m₁ + m₂). Отсюда вытекает:

r₁ r₂ r₁ = m₂r_o /(m₁ + m₂), r₂ = m₁r_o /(m₁ + m₂),

а I = m₁m₂r_o² /(m₁ + m₂) = Mr_o², где 1/M = 1/m₁ + 1/m₂. В данном случае М – приведенная масса.

Решение уравнения Шредингера обусловлено типом молекул: и зависит от соотношения I_a, I_b и I_c. Для вращательной энергии двухатомной молекулы решение имеет следующий вид:

E_j (Дж) = j(j+1)h²/8π²I_b,

где I_b = I, а вращательное квантовое число J принимает значения ряда положительных целых чисел: 0, 1, 2, 3, 4... Тогда уровни вращательной энергии, выраженные в виде волновых чисел в зависимости от J принимают следующие значения:

E_j /hC = Bj(j+1), j 0 1 2 3 4 5 6

где B = h/8π²I_bC E_j /hC 0 2Β 6Β 12Β 20Β 30Β 42Β

ν_излуч (см^-1) 2Β 4Β 6Β 8Β 10Β 12Β

Здесь В – вращательная постоянная.

9.3.2. Правила отбора.

9.3.2.1. По дипольному моменту молекулы μ (μ = le).

Для всех типов вращающихся молекул запрещены переходы, когда μ = 0.

Другими словами, излучению не с чем взаимодействовать, если молекулы не полярные, для которых вращательные спектры не наблюдаются

9.3.2.2. По вращательному квантовому числу.

Разрешены переходы, если Δj = +1.

Разрешенные переходы: 0 1, 1 2, 2 3 и т.д.

Вид спектра:

Таким образом, вращательная постоянная В находится из спектра как расстояние между двумя соседними линиями, а уже из нее вычисляют r_o.

9.3.3. Интенсивность полос спектра.

9.3.3.1. Вырождение уровней энергии.

Число вырожденных уровней N_j = 2j + 1.

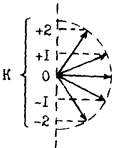
j = 2 j 0 1 2 3 4 Р – момент количества вращения

N_j 1 3 5 7 9 Р = Ιω = 2πν_врІ.

K – квантовое число момента

количества вращения вокруг оси

вращения или оси волчка.

выбранное направление, может стать реальным в

случае асимметричного волчка или опыта Штарка.

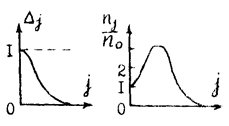
9.3.3.2. Распределение молекул по вращательным уровням.

Заселенность молекул по каждому вращательному энергетическому уровню определяется распределением Максвела – Больцмана:

Δ_j = exp(-BhCj(j+1)/ k_bT), где k_b – постоянная Больцмана.

Учитывая число вырожденных уровней N_j, получаем соотношение частиц на J-м и 0-м энергетическим уровням: n_j /n_o = (2j+1)Δ_j = N_j×Δ_j, что и демонстрируют приведенные ниже графики:

9.3.4. Нежесткий ротатор (учет колебания и вращения).

Решение уравнения Шредингера для вращения гармонического осцилятора:

E_j/hC = Bj(j+1) – Dj²(j+1)²,

где постоянная центробежного растяжения D определяется равенством:

D= h³/32π⁴I²r²kC (см^-1) = 16B³π²MC²/k.

Здесь k – силовая постоянная связи в свою очередь определяется уравнением:

k = 4π²C²M ν²_кол. Тогда D = 4B³/ ν²_кол, где ν_кол – волновое число колебания связи (см^-1). Поскольку D << B, то величиной D можно обычно пренебречь при j < 10.

Для ангармонического осцилятора в уравнение для энергии вводятся постоянные ангармоничности, коими в большинстве случаев также можно пренебречь.

Таким образом, для реальной двухатомной молекулы получают информацию в виде волнового числа ν_j(обр) = (Е_j+1 – E_j) /hC = 2B(j+1) – 4D(j+1)³. По любым трем смежным линиям спектра определяют j, B и D. Из В вычисляют значения r_o, а з D – величину ν_кол.

Дата добавления: 2014-01-05