Распределение Вейбулла- Гнеденко

Дифференциальная функция распределения имеет вид

f(t)=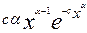, где с>0, α>0, 0<x<∞. (2.53)

Интегральная функция распределения:

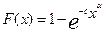, х>0. (2.54)

Если случайной величиной является время t, то (2.54) имеет вид

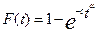, (2.55)

При α=l распределение Вейбулла—Гнеденко превращается в частный случай — показательное распределение.

Распределение (2.54) впервые экспериментально определено Вейбуллом, теоретическое его обоснование сделал Б. В. Гнеденко. Он также доказал, что это одно из распределений экспериментальных значений случайной величины. Вейбулл использовал это распределение для описания экспериментально определяемых разбросов прочности стали, границ ее прочности. Распределение Вейбулла—Гнеденко используется и при исследовании сроков службы радиоэлектронных приборов (α= 1,4...1.7).

Параметр α определяет формулу кривой f(t) и называется параметром формы. В общем случае величина α не превышает 2.

Параметр с определяет масштаб: при изменении с кривая f(t) растягивается или сжимается (рис 2.16).

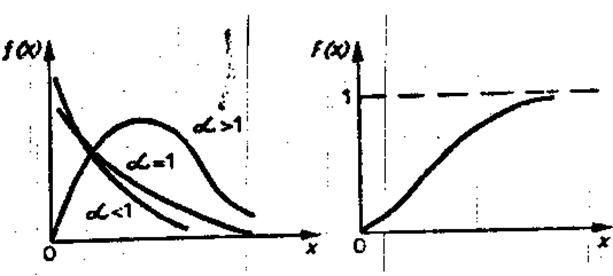
Рис. 2.16 Дифференциальная и интегральная функции распределения Вейбулла - Гнеденко

Вероятности безотказной работы за время t

p(t)=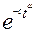, (2.56)

а интенсивность отказов λ(t)=c α t^{α -1}, и она снижается с ростом времени при α < 1 и возрастает при α > 1. Это обстоятельство позволяет использовать закон Вейбулла-Гнеденко при анализе надежности на всех этапах эксплуатации.

Дата добавления: 2014-01-05