Показательное распределение

ЛЕКЦИЯ №4.

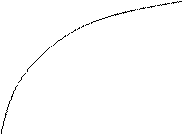
Показательным (экспоненциальным) называют распределение вероятностей, которое описывается дифференциальной функцией (рис. 2.15).

f(t)=λe^-λt, (2.47)

где λ — положительная постоянная величина, называемая параметром распределения.

Примером величины, распределенной по показательному закону, является время между двумя последовательными событиями простого (пуассоновского) потока.

Указанное распределение играет исключительную роль в теории надежности и практике расчетов. Например, выявлено, что во многих случаях промежутки времени между двумя последовательными отказами сложной системы распределены по показательному закону.

Интегральная функция распределения (рис. 2.15) имеет выражение

F(t)=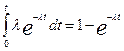. (2.48)

f(t) F(t)

1

0 t 0 t

рис. 2.15 Дифференциальная и интегральная функции показательного распределения вероятностей

Параметры показательного распределения — математическое ожидание, дисперсия и среднее квадратическое отклонение — однозначно выражаются через параметр λ;

M(t)=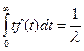; (2.49)

D(t)=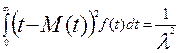; (2.50)

σ(t)=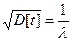. (2.51)

При рассмотрении надежности сложных объекте параметром λ является интенсивность отказов.

Вероятность того, что промежутки времени между двумя последовательными отказами сложной системы ограничены пределами t₁ и t₂, вычисляется следующим образом:

P(t₁< t <t₂)=F(t₂) - F(t₁)=(1-e^-λt2) – (1-e^-λt1)= e^-λt1 - e^-λt2 (2.52)

Дата добавления: 2014-01-05