Принадлежность прямой и точки плоскости

Плоскость. Способы ее задания, положение относительно плоскостей проекций

Положение плоскости в пространстве может быть однозначно определено:

- тремя точками, не лежащими на одной прямой;

- прямой и точкой, не лежащей на этой прямой;

- двумя параллельными прямыми;

- двумя пересекающимися прямыми;

- плоской фигурой;

- следом плоскости.

Всегда от одного способа задания плоскостей можно перейти к другому.

След плоскости – это линия пересечения заданной плоскости с одной из плоскостей проекций.

Соответственно различают горизонтальный, фронтальный и профильный следы плоскости.

Рис.3.5

Плоскостью общего положения называется плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций.

Плоскостями частного положения относительно плоскостей проекций называются плоскости параллельные или перпендикулярные им.

Плоскость перпендикулярная одной из плоскостей проекций называется проецирующей плоскостью.

Существует три вида проецирующих плоскостей: горизонтально-проецирующая, фронтально-проецирующая и профильно-проецирующая плоскости. Такие плоскости вырождаются в прямую линию (след плоскости) на ту плоскость проекций, к которой они перпендикулярны.

1. Горизонтально-проецирующая плоскость - плоскость перпендикулярная горизонтальной плоскости проекций.

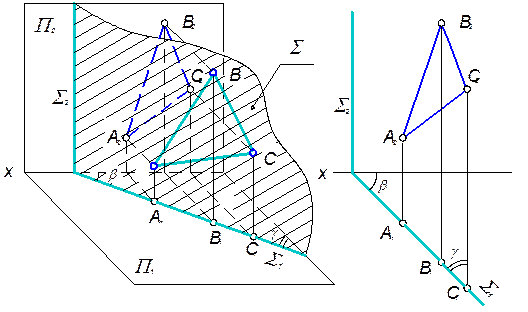
Рис. 3.6

2. Фронтально-проецирующая плоскость – плоскость перпендикулярная фронтальной плоскости проекций.

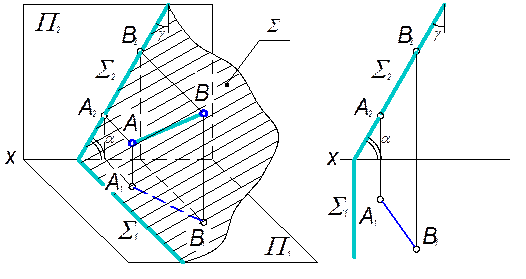
Рис. 3.7

3. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

Рис. 3.8

Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня.

Существует три вида плоскостей уровня: горизонтальная, фронтальная и профильная плоскости уровня.

1. Горизонтальная плоскость – плоскость, параллельная горизонтальной плоскости проекций.

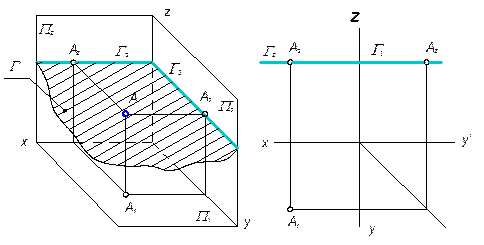
Рис. 3.9

2. Фронтальная плоскость - плоскость, параллельная фронтальной плоскости проекций.

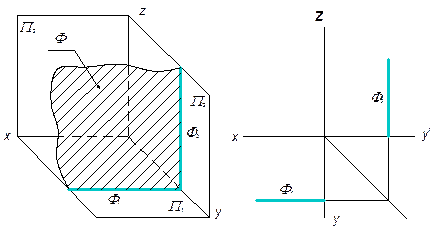
Рис. 3.10

3. Профильная плоскость – плоскость, параллельная профильной плоскости проекций.

Рис. 3.11

Возможны два случая расположения точки относительно плоскости: точка может принадлежать плоскости или не принадлежать ей (рис. 3.12).

Точка принадлежит плоскости, если принадлежит прямой, лежащей в этой плоскости.

Прямая принадлежит плоскости, если имеет с ней две общие точки или имеет с ней одну общую точку и параллельна другой прямой, лежащей в этой плоскости.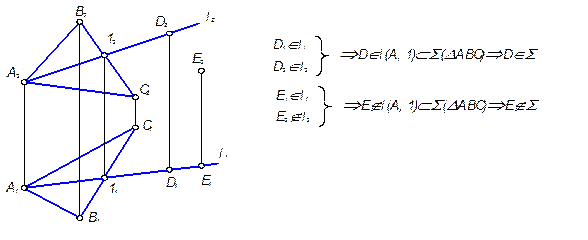

Рис. 3.12

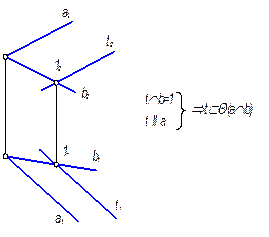
На рис. 3.12 изображена плоскость S(DАВС) и точки D и Е. Точка D принадлежит плоскости, т. к. принадлежит прямой l, имеющей с этой плоскостью две общие точки – 1 и А. Точка Е не принадлежит плоскости, т.к. через нее нельзя провести прямую, лежащую в данной плоскости. На рис. 3.13. показана плоскость Q(aÇb) и прямая t, лежащая в этой плоскости, т.к. имеет с ней общую точку 1 и параллельна прямой..

Рис. 3.13

Дата добавления: 2014-01-05