Взаимное расположение плоскостей

Параллельность прямой и плоскости

Взаимное расположение прямой и плоскости

Лекция №4

Для прямой и плоскости возможны три случая их взаимного расположения:

- прямая линия может принадлежать плоскости;

- быть параллельна плоскости;

- пересекаться с ней.

Задача принадлежности рассматривалась в § 3.3.

Прямая параллельна плоскости, если она параллельна прямой, принадлежащей этой плоскости.

Этот признак параллельности прямой и плоскости хорошо известен из курса стереометрии.

Рис. 3.16

Плоскости по отношению друг к другу могут занимать два положения: быть параллельными или пересекаться.

Плоскости параллельны, если пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым второй плоскости.

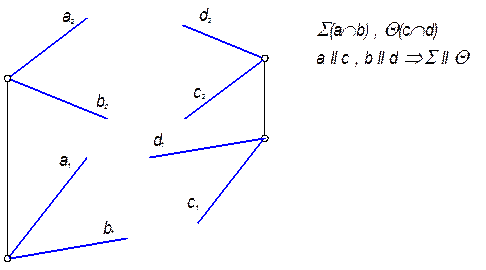
Рис. 3.11

Если две плоскости не параллельны, то они обязательно пересекаются и результатом их пересечения является прямая.

Для построения линии пересечения плоскостей необходимо найти две точки, одновременно принадлежащие этим плоскостям, или одну общую точку, если известно направление линии пересечения.

Направление линии пересечения известно в том случае, если:

1) пересекающиеся плоскости содержат взаимно-параллельные прямые (линия пересечения плоскостей параллельна этим прямым);

2) две пересекающиеся плоскости перпендикулярны третьей плоскости (линия пересечения перпендикулярна этой плоскости).

Общая точка для двух пересекающихся плоскостей в общем случае определяется с помощью вспомогательной плоскости частного положения, также пересекающей заданные плоскости по прямой (рис. 3.12).

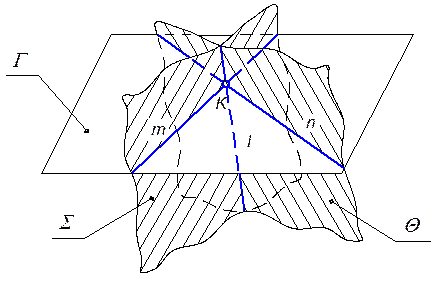
Рис. 3.12

Рассмотрим сначала частные случаи пересечение двух плоскостей:

1. Пересекаются плоскость общего положения Q (kÇm) горизонтально-проецирующая плоскость S (S₁), заданная следом.

Этот случай является основой для решения задач на пересечение плоскостей.

Т.к. одна из заданных плоскостей проецирующая, то все геометрические элементы, включая и линию пересечения плоскостей l, спроецируются на след этой плоскости. Т.е. горизонтальная проекция линии пересечения определяется исходя из принадлежности ее проецирующей плоскости S, а фронтальная проекция - по принадлежности второй заданной плоскости.

Рис. 3.13

2. Пересекаются плоскости общего положения заданные следами.

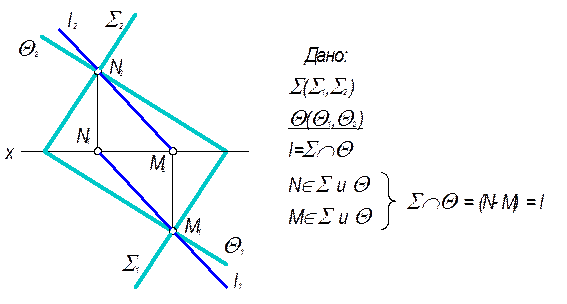
Рис. 3.14

В этом случае следы плоскости пересекаются в пределах чертежа, следовательно, линия пересечения этих плоскостей строится по двум точкам, являющимся следами линии пересечения, которые находятся в точках пересечения одноименных следов плоскостей.

Рассмотрим общий случай пересечения плоскостей:

3. Пересекаются плоскости общего положения.

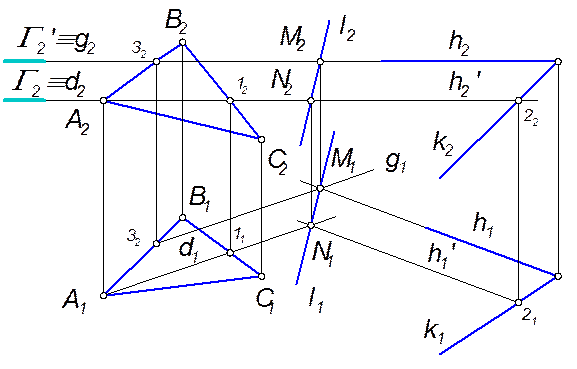
Рис. 3.15

Дата добавления: 2014-01-05