Структурный анализ механизмов и машин

Лекция № 1

Теория механизмов и машин – наука, изучающая общие методы структурного, кинематического и динамического анализа и синтеза различных механизмов, механику машин.

Знания, приобретенные при изучении , служат базой для курсов: детали машин, подъемно- транспортные машины, системы автоматизированного проектирования, проектирование специальных машин и др.

При анализе структурной схемы механизма определяют число подвижных звеньев, вид кинематических пар, число степеней свободы (подвижности), число замкнутых контуров и их класс, число избыточных контурных связей.

1.1 Машины и их классификация

Машина - устройство, выполняющее преобразование энергии, движения и информации, предназначенное для замены или облегчения физического или умственного труда человека. Машина обязательно совершает полезную работу. Существуют следующие виды машин: энергетические (двигатели, генераторы), транспортные, технологические и информационные (математические, контрольно – управляющие, кибернетические).

Машина осуществляет свой рабочий процесс посредством выполнения закономерных механических движений. Носителем этих движений является механизм.

1.2 Классификация механизмов

Механизм – система твердых тел, предназначенная для передачи и преобразования заданного движения одного или нескольких тел в требуемое движение других тел.

Механизмы не совершают полезной работы. Они предназначены только для осуществления требуемых законов движения их звеньев.

Машины и механизмы взаимно обратимы друг в друга. Так, напр., включенный, но не обрабатывающий деталь токарный станок является механизмом, но как только на нем начнется обработка детали, он сразу станет машиной.

Механизмы классифицируют по следующим признакам:

1. По области применения и функциональному назначению:

– механизмы д. в. с.;

– механизмы компрессоров и т. д.

2. По виду кинематических пар :

- с низшими ;

- с высшими .

3. По числу подвижности механизма;

4. По виду передаточной функции на механизмы:

- с постоянной передаточной функцией;

- с переменной передаточной функцией.

4. По движению и расположению звеньев в пространстве:

- пространственные;

- плоские.

5. По способу передачи и преобразования потока энергии:

- зацеплением;

- фрикционные;

- волновые.

6. По форме, конструктивному исполнению и движению звеньев:

- рычажные;

- зубчатые;

- кулачковые;

- планетарные.

Рис.1 Рычажные механизмы

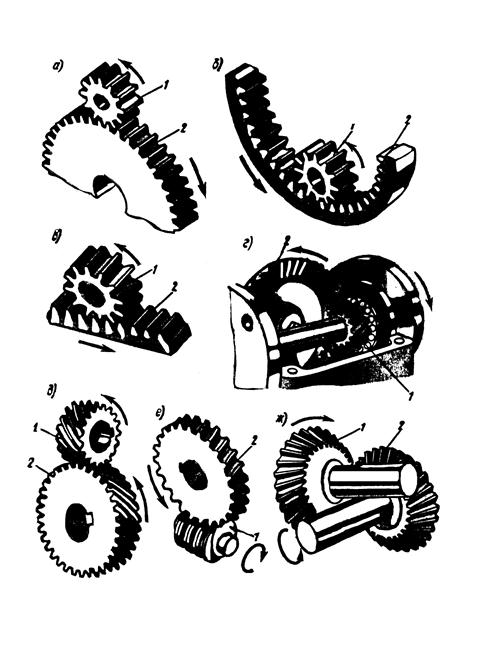
Рис.2 Зубчатые механизмы

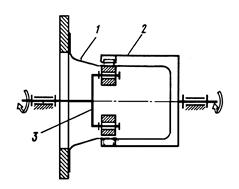
Рис.3 Волновой механизм

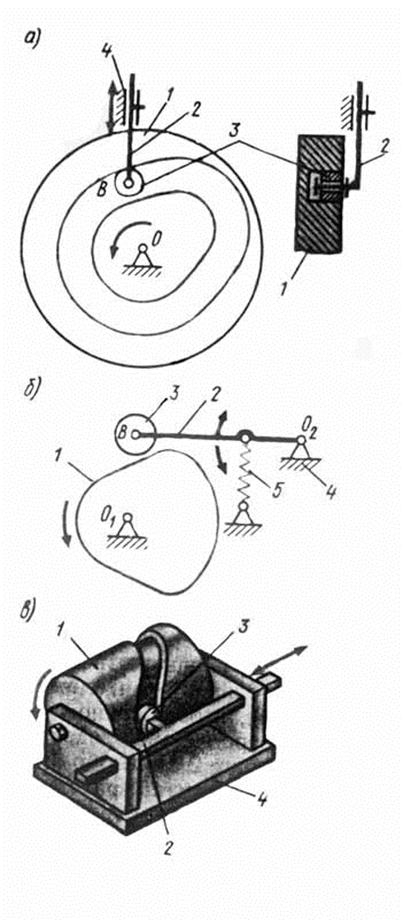
Рис.4. Кулачковые механизмы

Рис.5 Фрикционные механизмы

а) б)

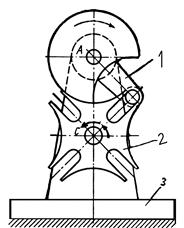
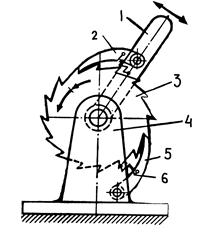
Рис.6 Механизмы с остановками выходного звена: мальтийский (рис.6,а), храповой (рис.6,б)

Безмасштабное графическое избражение механизма с применением условных обозначений звеньев и кинематических пар называют структурной схемой механизма.

Если структурную схему механизма выполнить в масштабе, то получим кинематическую схему механизма.

1.3 Основные понятия и определения строения механизмов

Всякий механизм состоит из деталей. Деталь – такая часть машины, которую изготовляют без сборочных операций. Звеном называется деталь или несколько неподвижно соединенных между собой деталей, движущихся как одно целое.

Звенья механизмов на схемах изображают упрощенно в виде линий или геометрических фигур.

Звенья ме6ханизма могут быть подвижными и неподвижными. Неподвижное звено называется стойкой. Обычно за стойку принимают корпус или раму машины, а также все жестко связанные с ними детали. Стойка в механизме всегда только одна.

Подвижные звенья бывают входными (ведущими ) и выходными (ведомыми ). Звено, которому сообщается движение, называется входным. Звено, которое осуществляет требуемое движение, для которого предназначен механизм, называется выходным. Все остальные звенья механизма называются промежуточными. Звено, координаты которого являются обобщенными для данного механизма, т.е. определяют движение всех остальных звеньев, называют начальным.

Чаще всего за начальное звено принимают входное звено, однако, не всегда. Обычно механизмы имеют один вход и один выход. Механизмы с одним входным звеном и несколькими выходными звеньями называют дифференциальными. Бывают механизмы с несколькими входными звеньями и одним выходным. Последние механизмы называют суммирующими.

Подвижные звенья, в зависимости от вида их движения и назначения, имеют определенные названия (кривошип, шатун, коромысло, кулиса, ползун, камень, кулачок, зубчатое колесо и т.п.).

Кривошип – вращающееся звено механизма, которое совершает полный оборот вокруг оси, связанной со стойкой.

Шатун – звено механизма, образующее кинематические пары только с подвижными звеньями.

Коромысло – звено механизма, которое совершает только колебательные движения при неполном вращении вокруг неподвижной оси, связанной со стойкой.

Ползун – звено, образующее поступательную пару со стойкой.

Кулиса – подвижное звено механизма, являющееся направляющей для камня.

Камень – звено, образующее поступательную пару с кулисой.

Кулачок – звено, имеющее рабочий профиль переменной кривизны.

На структурных схемах звенья механизмов обозначают арабскими цифрами. Стойка обозначается штриховкой под углом и (или) цифрой ноль ().

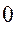Подвижное соединение двух соприкасающихся звеньев называют кинематической парой. Для существования кинематической пары необходимы следующие условия:

- наличие двух звеньев;

- постоянное соприкосновение этих звеньев;

- возможность их относительного перемещения.

Замыкание кинематических пар может быть геометрическим или силовым, напр., с помощью собственной массы, пружин и т.п.

Звенья при объединении их в кинематическую пару взаимодействуют между собой по поверхностям, линиям и точкам.

Совокупность поверхностей, линий или точек звена, которые будут контактировать с другим звеном, образуя кинематическую пару, называют элементом кинематической пары.

Система звеньев, связанных между собой кинематическими парами, называется кинематической цепью. В основе всякого механизма лежит кинематическая цепь.

1.4 Кинематические пары и их классификация

В зависимости от вида контакта элементов кинематических пар, различают высшие и низшие кинематические пары.

Кинематические пары, образованные элементами в виде линии или точки, называются высшими.

Кинематические пары, образованные элементами в виде поверхностей, называются низшими.

Кинематические пары также разделяют:

-по числу (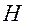) степеней свободы (подвижности (), которые они представляют соединенным звеньям;

- числу () условий связей (класс пары), налагаемых парой на относительное движение соединяемых звеньев;

- виду реализуемых в них простейших независимых движений.

На рис. 7,8 представлены примеры кинематических пар различных классов и видов.

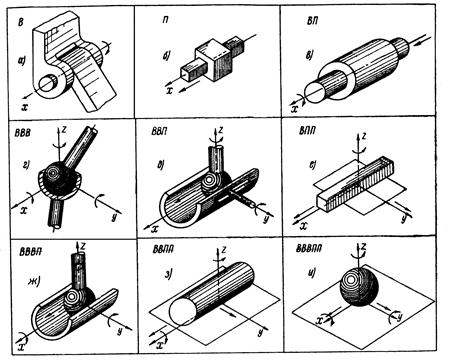
Рис.7

Примеры кинематических пар

1.Вращательная низшая одноподвижная

2 Поступательная низшая одноподвижная

3. Цилиндрическая низшая двухподвижная

4. Сферическая низшая трехподвижная

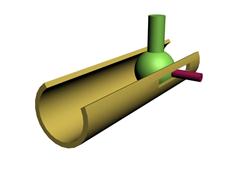
5. Сферическая с пальцем низшая трехподвижная КП (ВВП)

6.Плоскостная низшая трехподвижная

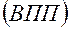
7. Цилиндр – плоскость (Высшая четырехподвижная

8. Шар – плоскость (Выысшая пятиподвижная

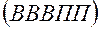
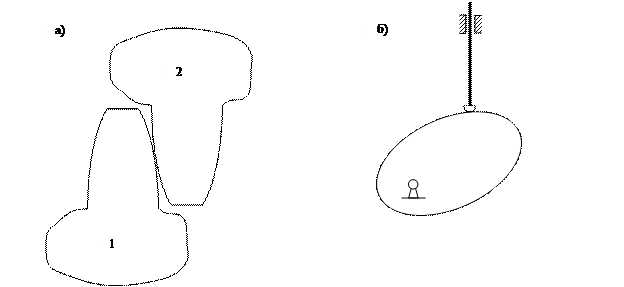
Рис. 8 Примеры высших кинематических пар: а – зубья зубчатых колёс; б – кулачок и толкатель кулачкового механизма

Всякое тело, свободно движущиеся в пространстве, обладает шестью степенями свободы, т.е. движение может быть представлено как вращение вокруг трех осей и поступательное движение вдоль этих же осей (рис.3).

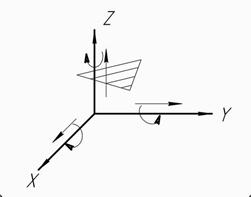
Рис.9 Число степеней свободы любого тела в пространстве

Для звена, входящего в кинематическую пару, число условий связи, наложенных на относительное движение звеньев, находится в пределах:

,

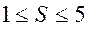где – число условий связи.

Поскольку число связей меняется от 1 до 5, существует 5 классов кинематических пар (табл.1).

Все пары 5-го класса - низшие (поступательная, вращательная, винтовая). Различают одноподвижные пары (Vкласса, Н =1, S =5), двухподвижные (1Vкласса, Н =2, S =2), трехподвижные (111 класса, Н=3, S = 3), четырехподвижные (11 класса, Н =4, S =2) и пятиподвижные (1 класса, Н = 5, S =1)

На структурных схемах механизмов кинематические пары обозначают большими латинскими буквами.

Таблица 1

№п/п	Рисунок	Название пары	Условное обозначение	Подвижность	Высшая низшая	геометрическая силовая
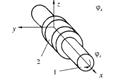
		Вращательная			Н	Г
		Поступательная			Н	Г
		Винтовая			Н	Г
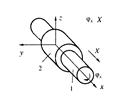
		Цилиндрическая		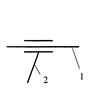	Н	Г
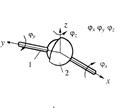
		Сферическая			Н	Г С
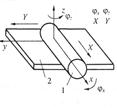
		Цилиндр - плоскость		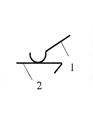	В	С
		Шар - плоскость		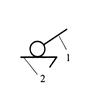	В	С

1.5 Кинематические цепи. Структурная формула кинематической цепи

Кинематические цепи различают по следующим признакам (рис.10):

а) замкнутые и незамкнутые;

б) простые и сложные;

в) плоские и пространственные.

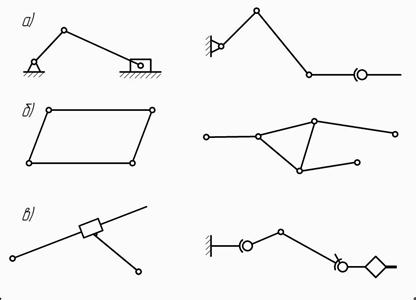
Рис.10 Кинематические цепи

В замкнутой цепи каждое звено входит не менее чем в две кинематические пары; в незамкнутой цепи есть звенья, входящие только в одну кинематическую пару. В простой цепи каждое звено входит не более чем в две кинематические пары; в сложной цепи есть звенья, входящие более чем в две кинематические пары.

В плоской цепи все звенья перемещаются в одной плоскости либо в параллельных плоскостях; в пространственной – звенья движутся в разных, непараллельных плоскостях.

Структурная формула кинематической цепи связывает число степеней свободы с числом и видом кинематических пар в данной кинематической цепи.

Пусть в механизме, имеющем звеньев (включая стойку), 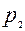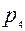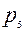_, , , , – число одно-, двух-, трех-, четырех- и пятиподвижных пар. Число подвижных звенев обозначим . Если бы все подвижные звенья были свободными телами, общее число степеней свободы было бы равно . Однако каждая одноподвижная пара V класса накладывает на относительное движение звеньев, образующих пару, 5 связей, каждая двухподвижная пара 1V класса – 4 связи и т. д. Следовательно, общее число степеней свободы кинематической цепи 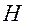в общем случае определяется соотношением:

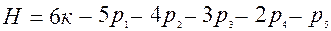_. (1.1)

Степень подвижности механизма (W) относительно стойки определяется по формуле:

_. (2.2)

Полученная формула называется структурной формулой кинематической цепи и носит имя А.П. Малышева.

Если наложить три общих связи получим плоский механизм. Структурная формула кинематической цепи в этом случае принимает вид:

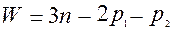(1.3)

и называется формулой Чебышева для плоских механизмов.

В плоских механизмах все одноподвижные пары являются низшими парами, а двухподвижные – высшими парами. Поэтому формулу Чебышева можно представить в виде:

, (1.4)

где - число подвижных звеньев;

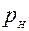– число низших пар;

– число высших пар.

Примеры определения подвижности различных механизмов.

Пример 1. Найдем подвижность шарнирного четырехзвенного механизма (рис.11).

Рис. 11 Шарнирный четырехзвенный механизм

Механизм имеет три подвижных звена (n = 3) и четыре низших кинематических пар (р_Н =4 (А, В, С, Д). Значит, его подвижность по формуле Чебышева будет

Пример 2 (рис.12)

Рис.12

По формуле Чебышева: n=5 (1, 2, 3, 4, 5), р₁ =7 (0-1, 1-2, 2-3, 3-4, 4-0, 3-5, 5-0), р₂ =0. Следовательно,

W= 3n – 2p₁ – p₂ = 3 · 5- 2 · 7 – 0 = 1.

Дата добавления: 2014-01-05