Лекция №3. Основные положения теории информации

Основные положения теории информации были разработаны К. Шен­ноном[ ] в его работах 1948, 1949 и 1950 годов. «Основная идея теории информации состоит в том, что с информацией можно обращаться почти так же, как с такими физическими величинами, как масса или энергия». Поэтому система транспортировки инфор­мации может рассматриваться подобно системам транспортировки массы или энергии.

3.2.Понятие энтропии

Понятие энтропии (теорема 2). Выше речь шла о числовых харак­теристиках законов распределения погрешностей, которыми поль­зуются в теории вероятностей. Энтропи́я (от др.-греч. ἐντροπία - поворот, превращение) — в естественных науках мера беспорядка системы, состоящей из многих элементов. В теории информации — мера неопределённости какого-либо опыта (испытания), который может иметь разные исходы, а значит, и количество информации

Для теории информации К. Шеннон предложил систему критериев, кратко описывающих законы распределения. Для харак­теристики систематической составляющей используется, как и прежде, первый начальный момент, т. е. значение математического ожидания, а для характеристики центрированной случайной составляющей вместо всех моментов более высоких порядков используется своеобразный момент, равный для закона распределения р (х) интегралу

Н(Х) = -p(x)ln p(x)dx (3.1)

и называемый энтропией. Таким образом, энтропия является функцио­налом закона распределения случайной величины и учитывает особен­ности этого закона.

Единицы измерения энтропии. Единицы измерения энтропии зави­сят от выбора основания логарифма в приведенных выражениях. При использовании десятичных логарифмов энтропия определяется в так называемых десятичных единицах (дит). В случае же двоичных логарифмов энтропия выражается соответственно в двоичных едини­цах (бит). Бит – (binary digit) количество информации, которое содержится в сообщении о том, что объект находится в одном из двух равновероятных состояниях.

Недостаток – при таком определении полностью игнорируется смысловой контекст информации.

В математических выкладках более удобно использовать натуральные логарифмы.* При анализе электронных вычислительных машин или приборов, работающих в двоичной системе счисления, удобнее пользоваться двоичными единицами, а при анализе измери­тельных устройств, работающих, как правило, в десятичной (или двоично-десятичной) системе счисления, — десятичными единицами.

Понятие условной энтропии, или энтропии помехи. В теоремах 10 и 16 Шеннон показывает, что дезинформационное действие случайной погрешности, шума или помех при передаче сигнала определяется энтропией шума как случайной величины. В теореме 16 он указывает, что если шум в вероятностном смысле не зависит от передаваемого сигнала, то независимо от статистики сигнала шуму можно приписать определенную величину энтропии, которая и характеризует его дезин­формационное действие. Это очень важное положение, так как точный анализ суммы сложного сигнала и шума математически весьма труден. На основе же 16-й теоремы Шеннона этот анализ (при статистически независимом шуме) можно вести раздельно для сигнала и шума, что резко упрощает решение такой задачи.

Теорема 10 по формулировке относится к теории кодирования, однако по существу она является доказательством предыдущего положения.

* Исторически первоначально для двоичных и десятичных единиц энтропии были предложены сокращенные обозначения в виде binit и decit, однако при упот­реблении обозначение двоичной единицы было сокращено до bit (по-русски бит), а десятичной и натуральной единиц — до dit (дит) и nit.

Здесь утверждается, что количество передаваемой информа­ции I равно энтропии передаваемого сигнала Н (X) за вычетом энтро­пии шума Н (Δ), т. е.

I=H (X) - H (Δ) .* (3.2)

* Здесь и далее обозначения Н (X) или Н (Δ) не являются функциями Н от случайной величины Х или Δ, а представляют собой обозначения энтропии случай­ных величин Х и Δ.

3.2. Применение основных положений теории информации для характеристики процесса измерения

Точность измерений мы обычно харак­теризуем числовым значением полученных при измерении или пред­полагаемых погрешностей. При этом используются понятия абсолют­ной и относительной приведенной погрешностей. Если измерительное устройство имеет диапазон измерения от Х ₁ до Х ₂, т. е. может измерять величины, находящиеся в пределах от X ₁ до Х ₂, с абсолютной погреш­ностью ± Δ, не зависящей от текущего значения х измеряемой вели­чины, то, получив результат измерения в виде показания Х _П, записы­ваем его как Х _П ± Δ и характеризуем относительной приведенной погрешностью

(3.3)

Рассмотрение этих же самых действий с позиций теории информации носит несколько иной характер, отличающийся тем, что всем перечис­ленным понятиям придается вероятностный, статистический смысл, а итог проведенного измерения истолковывается как сокращение области неопределенности измеряемой величины. В теории информа­ции тот факт, что измерительный прибор имеет диапазон измерений от Х ₁ до X ₂, означает, что при использовании этого прибора могут быть получены показания Х _П только в пределах от Х ₁ до Х ₂. Другими сло­вами, вероятность получения отсчетов, меньших Х ₁ и больших X ₂, равна нулю. Вероятность же получения отсчета где-то в пределах от Х ₁ до Х ₂ равна единице.

Если предположить, что плотность вероятности распределения различных значений измеряемой величины вдоль всей шкалы прибора одинакова, то с точки зрения теории информации наше знание о значе­нии измеряемой величины до измерения может быть представлено гра­фиком распределения плотности вероятности р (х) вдоль шкалы зна­чений х, показанным на рис. 3.1.

Так как полная вероятность.получить отсчет где-то в пределах от Х ₁ до X ₂ равна единице, то под кривой р (х) должна быть заключена площадь, равная единице (условие нормирования). При равномерном распределении плотности вероятности это приводит к

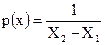(3.4)

После проведения измерения получаем показание прибора, равное Х _П. Однако вследствие погрешности прибора, равной ±Δ, мы не мо­жем утверждать, что измеряемая величина точно равна значению Х _П. Поэтому записываем результат измерения в виде Х _П ± Δ. Это озна­чает, что действительное значение измеряемой величины Х лежит где-то в пределах от Х _П + Δ до Х _П —Δ, т. е. в пределах участка 2Δ, как показано на рис. 3.1.

С точки зрения теории информации результат нашего измерения состоит лишь в том, что до измерения область неопределенности про­стиралась от X ₁ до X ₂ и характеризова­лась

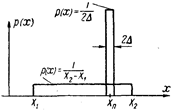
малой плотностью вероятности р (х) = 1/(Х ₂ — X ₁), а после измерения она сократилась до величины 2Δ и ха­рактеризуется намного большей плотно­стью вероятности р (х) = 1/2Δ.

Рис. 3.1

Дата добавления: 2014-01-05