Прохождение микрочастиц сквозь потенциальный барьер

Допустим, что область, где может двигаться микрочастица, разделена на две части потенциальным барьером. Таким, например, может быть движение електрона при переходе его из метала в вакуум: на границе он встречает потенциальный бартер, преодоление котрого связано с совершением работы выхода.

Схема потенциального барьера, имеющего ширину «d» и высоту «U» изображена на рисунке.

По классическим представлениям поведение частицы имеет следующий характер: если энергия частицы больше высоты барьера (E>U), то частица беспрепятственно проходит над барьером. Если же E<U, то частица отражается от барьера и летит в обратную сторону.

Совершенно иначе выглядит поведение частицы согласно квантовой механике:

во-первых, даже при E >U имеется отличная от нуля вероятность того, что частица отразится от барьера и полетит в обратную сторону;

во-вторых, при E < U имеется отличная о нуля вероятность того, что частица проникнет сквозь барьер и окажется в области, где . Такое, совершенно невозможное с классической точки зрения поведение микрочастицы, вытекает непосредственно из уравнения Шредингера.

Расчет показывает, что вероятность просачивания частицы через барьер может быть выражена формулой

,

где 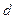- ширина;

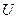- высота барьера;

- полная энергия частицы.

Как видно из этой формулы, чем больше ширина и высота барьера, а также, чем больше масса микрочастицы, тем меньше вероятность прохождения ее через барьер. Это явление прохождения микрочастицы через потенциальный барьер носит название туннельного эффекта.

С классической точки зрения туннельный эффект представляется абсурдным, так как находящаяся в туннеле частица имеет E<U, и, следовательно, должна иметь отрицательную кинетическую энергию. В квантовой механике деление полной энергии на кинетическую и потенциальную не имеет смысла и противоречит принципу неопределенности. Это видно из того, что если бы частица обладала определенной кинетической энергией, то она имела бы определенный импульс . Аналогично, если частица имеет определенную потенциальную энергию, то значит, она находится в точно заданном месте пространства. Поскольку координата и импульс частицы не могут одновременно иметь определенных значений, то не могут быть точно определены кинетическая и потенциальная энергия частицы. Таким образом, хотя полная энергия частицы имеет вполне определенное значение, она не может быть представлена в виде суммы точно определенных значений кинетической и потенциальной энергии. Следовательно, говорить о том, что частица, находящаяся в туннеле, обладает отрицательной кинетической энергией, с точки зрения квантовой механики, не имеет смысла.

Дата добавления: 2014-01-05