Пример решения задачи о назначениях

Пусть в виде таблицы дана матрица 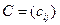несоответствия «претендентов» 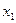,,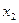,,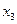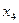имеющимся «должностям» ,,,,():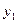

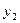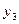Таблица 1.

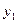
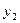
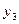
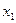
	^7	^2	^1	^9	^4
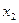
	^9	^6	^9	^5	^5
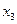
		^8	^3	^1	^8
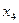
	^7	^9	^4	^2	^2
	^8	^4	^7	^4	^8

Если вначале дана матрица соответствия 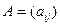, то элементы матрицы 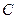определим по формулам .

Определим начальные значения потенциалов, положив и 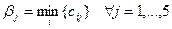. Другими словами, потенциал положим равным наименьшему из тарифов в 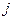- том столбце. Нетрудно проверить, что так определенные потенциалы удовлетворяют условиям: 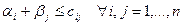, поскольку . Значения потенциалов запишем в добавленный справа к таблице столбец, а потенциалов в добавленную снизу строку. Кроме того, в клетки таблицы, удовлетворяющие условию 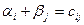запишем «потенциальные» единицы.

Таблица 2.

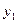
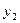
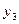
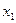
	^7	1 ^2	1 ^1	^9	^4
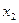
	^9	^6	^9	^5	^5
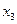
	1 ^3	^8	^3	1 ^1	^8
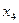
	^7	^9	^4	^2	1 ^2
	^8	^4	^7	^4	^8

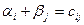Очевидно, что в силу определения и равенство будет выполняться в тех клетках 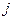- того столбца, в которых значение тарифа является наименьшим в соответствующем столбце (именно в этих клетках мы и поставили единицы). Заметим, что если бы оказалось ровно по одной единице в каждом столбце и в каждой строке, то есть всего 5 допустимых единиц, то согласно п.7.3 мы получили бы оптимальное решение задачи, положив 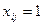для соответствующих допустимых единиц (а все остальные 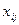полагая равными нулю). Выберем теперь из имеющихся 6 потенциальных единиц максимально возможное число единиц так, чтобы в каждом столбце и в каждой строке стояло не более одной (допустимой) единицы. Разумеется, это можно сделать методом полного перебора, но мы хотим указать не метод «тыка», а способ, дающий эффективное решение задачи выбора допустимых единиц, основванный на известном алгоритме Форда-Фалкерсона. Для этого будем считать переменные 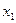,,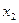,,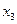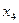и 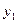,,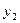,,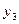вершинами некоторой сети. Снабдим эту сеть (фиктивным) входом 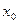и (фиктивным) выходом , соединив вход дугами с вершинами 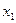,,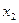,,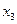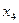и вершины 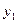,,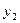,,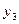с выходом (см. рис. 1). Кроме того, каждой потенциальной единице, стоящей в 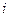-той строке и 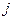-том столбце таблицы 2, сопоставим дугу с началом 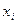и концом 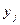. В результате получим следующую сеть.

Рис.1. Сеть для таблицы 2.

Кроме того, в таблицу снизу добавлена строка для определяемой ниже невязки и одна вспомогательная строка, смысл которых прояснится в дальнейшем и

С помощью условия (3) определим заполненные клетки таблицы. В первом столбце (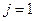) равенство 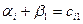будет иметь место

добавив столбец для переменных , строку для переменных и две специальных строки, назначение которых станет ясно

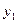
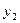
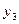
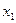
	^7	^2	^1	^9	^4
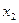
	^9	^6	^9	^5	^5
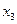
	^7	^8	^3	^1	^8
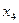
	^7	^9	^4	^2	^2
	^8	^4	^7	^4	^8
невязка
строка

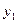
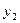
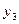
						α
α1	^7	1^2	1^1	^9	^4
α2	^9	^6	^9	^5	^5
α3	1 ^3	^8	^3	^1	^8
α4	^7	^9	^4	^2	1^2
α5	^8	^4	^7	^4	^8
min βj
невязка
строка

Дата добавления: 2014-01-05