Прямо-двойственный метод решения задачи о назначениях

Задача о назначениях как транспортная задача.

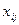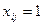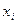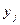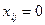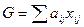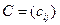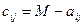Определим значения переменных следующим образом: , если назначается на должность , и в противном случае. Тогда функция соответствия имеет вид . Если матрицу соответствия заметить на матрицу несоответствия , где и 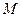- некоторая константа, то задача состоит в таком выборе должностей 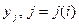, чтобы цена несоответствия 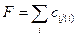была минимальной. Таким образом, модель задачи о назначениях принимает вид:

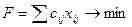
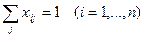(1)

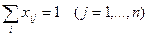
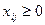
Таким образом, получается частный случай замкнутой (закрытой) модели транспортной задачи. Следовательно, задача о назначениях всегда имеет решение. Случай открытой модели, как обычно, сводится к замкнутому.

Транспортная задача (1) может быть решена методом потенциалов, причем ее решение окажется, очевидно, целочисленным. Из вида ограничений в (1) следует, что для каждого ровно одна из целочисленных переменных 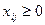равна 1, а остальные равны 0 (и аналогично для каждого 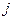ровно одна из целочисленных переменных 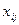равна 1, а остальные равны 0). Следовательно, число ненулевых переменных 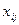(число «заполненных» клеток в транспортной таблице) равно 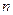, в то время как ранг задачи (число базисных переменных) равен 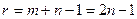. Задача получается сильно вырожденной, и для ее решения методом потенциалов потребуется вводить в рассмотрение 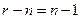«базисных нулей», что осложняет решение.

Изложим теперь суть прямо-двойственного метода решения задачи (1). Также как и в методе потенциалов рассматриваются двойственные переменные 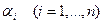и 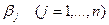, удовлетворяющие ограничениям двойственной задачи:

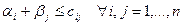. (2)

(мы не выписываем целевой функции двойственной задачи, поскольку она нам не понадобится). Отметим, что в отличие от метода потенциалов эти условия выполняются на каждом шаге решения задачи, а не только на последнем, когда найдено оптимальное решение. С другой стороны, в методе потенциалов условие

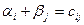(3)

имеет место 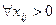и служит для определения самих потенциалов, а в прямо-двойственном методе, наоборот, это условие служит для определения «заполненных» клеток транспортной таблицы, соответствующих ненулевым переменным 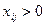. Таким образом, «ход мысли» здесь противоположен методу потенциалов.

Как было уже замечено выше, из условия 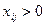следует, что, на самом деле, 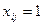, причем в этом случае все остальные переменные 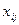в 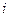- ой строке и 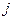-ом столбце равны нулю. Будем для удобства называть такие 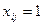«возможными единицами». Ясно, что выполнение ограничений задачи (1) равносильно существованию ровно 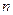возможных единиц. Хорошо известно, что допустимые решения исходной транспортной задачи (1) и соответствующей двойственной задачи будут оптимальны, если для всех 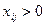выполнены условия 2-ой теоремы двойственности 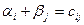. Итак, оптимальное решение будет получено, если удастся отыскать ровно 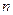допустимых единиц, определяемых условием .

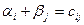Прямо-двойственный метод именно это и позволяет сделать. Для простоты изложим его на конкретном примере.

Дата добавления: 2014-01-05