
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определения и основные понятия
Определение 1. Паросочетанием на графе 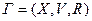 , называется такое подмножество
, называется такое подмножество 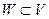 , что, если
, что, если 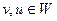 , то
, то 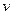 и
и 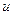 не имеют общих вершин.
не имеют общих вершин.
Рис. 1. 
|


|
|
|




|
|
|
| ||||
|
В графе на рис.1 имеются паросочетания: 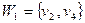 ,
, 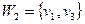 ,
, 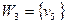 .
.
Определение 2. Число 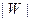 ребер в паросочетании
ребер в паросочетании 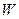 называется мощностью паросочетания.
называется мощностью паросочетания.
В приведенном выше примере 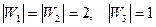 .
.
Определение 3. Паросочетание 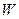 называется максимальным, если из того, что
называется максимальным, если из того, что 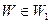 и
и 
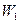 – паросочетание, следует, что
– паросочетание, следует, что 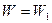 .
.
Замечание 1. В силу конечности графа 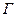 в нем существует паросочетание максимальной мощности, которое, очевидно, является максимальным. Однако, существуют максимальные паросочетания не максимальной мощности, например, паросочетание
в нем существует паросочетание максимальной мощности, которое, очевидно, является максимальным. Однако, существуют максимальные паросочетания не максимальной мощности, например, паросочетание 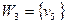 в рассмотренном выше примере 1.
в рассмотренном выше примере 1.
Замечание 2. Одной из типичных задач теории графов является задача нахождения паросочетания наибольшей мощности.
Определение 4. Весом или нагрузкой на графе 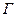 называется неотрицательная функция
называется неотрицательная функция 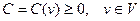 на множестве
на множестве 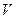 ребер графа
ребер графа 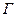 . Граф
. Граф 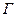 с весом
с весом 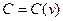 будем называть нагруженным графом.
будем называть нагруженным графом.
Определение 5. Весом 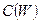 паросочетания
паросочетания 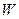 в нагруженном графе
в нагруженном графе 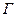 называется сумма весов всех ребер паросочетания
называется сумма весов всех ребер паросочетания 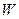 :
: 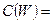
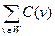 .
.
Определение 6. Паросочетание 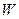 максимального веса назовем максимальным.
максимального веса назовем максимальным.
Замечание 3. Ранее в определении 3 мы определили паросочетание максимальное в теоретико-множественном смысле. Начиная с этого места максимальным будем называть только паросочетание максимального веса. В силу неотрицательности веса паросочетание максимального веса будет, очевидно, максимальным и в теоретико - множественном смысле.
Далее мы рассматриваем задачу отыскания максимального паросочетания в нагруженном графе 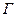 :
: 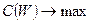 , где
, где 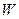 - паросочетание в
- паросочетание в 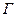 .
.
Замечание 4. Рассмотренная ранее задача отыскания паросочетания максимальной мощности является частным случаем задачи отыскания максимального паросочетания в нагруженном графе 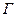 с весом
с весом 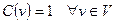 (вес паросочетания в этом случае совпадает с его мощностью).
(вес паросочетания в этом случае совпадает с его мощностью).
Определение 6. Граф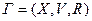 называется двудольным, если множество его вершин
называется двудольным, если множество его вершин 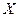 можно разбить на доли
можно разбить на доли 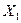 и
и 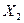 так, что
так, что 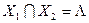 , где
, где 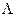 - пустое множество,
- пустое множество, 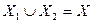 и, если вершины
и, если вершины 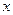 и
и 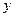 – смежные, то либо
– смежные, то либо 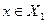 и
и 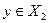 , либо
, либо 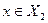 и
и 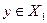 .
.
Двудольный граф будем записывать в виде 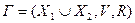 .
.
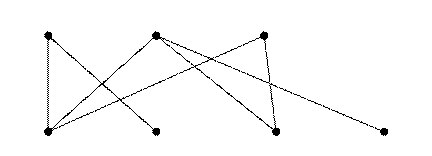 Рис. 2. Двудольный граф.
Рис. 2. Двудольный граф.
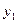
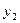
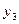
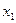
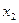
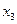
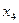
Определение 7. Двудольный граф 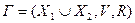 называется полным двудольным графом, если любые две вершины
называется полным двудольным графом, если любые две вершины 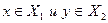 - смежные.
- смежные.
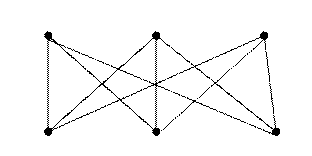 Рис. 3. Полный двудольный граф
Рис. 3. Полный двудольный граф 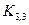 , с
, с 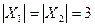 .
.
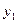
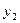
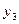
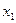
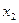
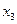
Пусть дана матрица 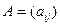 соответствия «претендентов»
соответствия «претендентов» 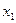 ,
,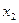 ,…,
,…,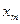 имеющимся «должностям»
имеющимся «должностям» 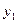 ,
,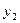 ,…,
,…,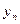 . Задача о назначениях состоит в определении оптимального выбора должности для каждого претендента. Критерием служит суммарная цена соответствия претендентов занимаемым должностям. Если на соответствующем (двудольном) графе для каждого
. Задача о назначениях состоит в определении оптимального выбора должности для каждого претендента. Критерием служит суммарная цена соответствия претендентов занимаемым должностям. Если на соответствующем (двудольном) графе для каждого 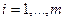 выделить дугу
выделить дугу 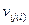 , соответствующую назначению
, соответствующую назначению 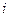 -го претендента на
-го претендента на 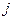 -ую должность то получим паросочетание веса
-ую должность то получим паросочетание веса 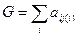 . Таким образом, задача о назначениях сводится к задаче об оптимальном паросочетании. На рис. 4 представлено паросочетание на графе
. Таким образом, задача о назначениях сводится к задаче об оптимальном паросочетании. На рис. 4 представлено паросочетание на графе 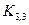 с весом (ценой соответствия)
с весом (ценой соответствия) 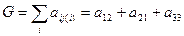 .
.
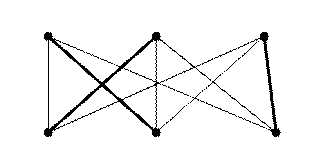 Рис. 4. Задача о назначениях для
Рис. 4. Задача о назначениях для 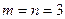
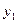
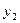
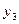
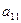
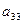
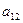
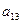
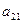
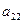
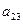
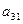
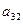
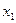
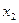
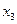
Далее для простоты рассматриваем случай 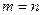 .
.
|
Дата добавления: 2014-01-05; Просмотров: 296; Нарушение авторских прав?; Мы поможем в написании вашей работы!