Методы коррелирования рядов динамики

Если оба ряда динамики лишены автокорреляции, то значения уровней каждого из них в отдельности являются такими же независимыми, как значения признаков у различных единиц статистической совокупности. Поэтому в этом случае для оценки взаимосвязи используют те же показатели, что и для признаков, – парный коэффициент корреляции и корреляционное отношение.

Например, если эмпирическая кривая, описывающая зависимость уровней одного ряда от другого, указывает на линейную корреляцию, то рассчитывают парный коэффициент корреляции:

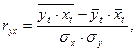
где y_t, x_t – уровни исследуемых рядов динамики;

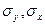- их среднеквадратичное отклонение.

Интерпретация этого коэффициента ничем не отличается от его интерпретации для статистических признаков.

Аналогично поступают для нелинейной корреляции, рассчитывая корреляционное отношение (см. раздел ”Парная корреляция статистических признаков”).

При наличии автокорреляции хотя бы в одном из исследуемых рядов динамики для оценки их взаимосвязи используют один из двух методов.

1. Метод коррелирования отклонений, когда коррелируют не сами уровни, а их отклонения от основной тенденции, а при ее отсутствии – от среднего уровня.

Вначале для каждого ряда определяют уравнение тренда или средний уровень. Затем из фактических уровней вычитают уровни тренда или средний уровень:

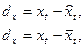
Далее оценивают тесноту связи между рядами, рассчитывая коэффициент корреляции отклонений:

Его величина изменяется от -1 до 1. Знак указывает на направление связи: отрицательный – обратная, положительный – прямая. Чем ближе абсолютное значение этого коэффициента к 1, тем сильнее связь.

2. Метод коррелирования разностей, когда коррелируют разности уровней – первые, вторые и так далее.

При линейной тенденции рассчитывают только первые разности – абсолютные приросты уровней:

Затем рассчитывают коэффициент корреляции разностей:

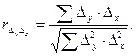
Он принимает значения от -1 до 1 и интерпретируется аналогично коэффициенту корреляции отклонений.

При параболической тенденции на основе первых разностей рассчитывают вторые:

Затем в формулу для расчета коэффициента корреляции вместо первых разностей подставляют вторые.

Дата добавления: 2014-01-05