Равномерное вращение сосуда с жидкостью

Возьмем открытый цилиндрический сосуд с жидкостью и сообщим ему вращение с постоянной угловой скоростью w вокруг его верти­кальной оси. Жидкость постепенно приобретет ту же угловую ско­рость, что и сосуд, а свободная поверхностьее видоизменится; в цент­ральной части уровень жидкости понизится, у стенок — повысится, и вся свободная поверхность жидкости станет некоторой поверх­ностью вращения (рис. 1.18).

На жидкость в этом случае будут действовать две массовые силы — сила тяжести и центробежная сила, которые, будучи отне­сенными к единице массы, соответственно равны g и .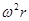

Равнодействующая массовая сила j увеличивается с увеличением радиуса за счет второй составляющей, а угол наклона ее к горизонту уменьшается. Эта сила нормальна к свободной поверхности жидко­сти, поэтому наклон этой поверхности с увеличением радиуса воз­растает. Найдем уравнение кривой АОВ в системе координат z и r с началом в центре дна сосуда. Учитывая, что сила j является нормалью к кривой АОВ, из чертежа находим

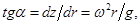
откуда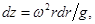

или после интегрирования

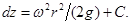
В точке пересечения кривой АОВ с осью вращения r = 0, z = h= C, поэтому окончательно будем иметь

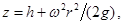(1.34)

т. е. кривая АОВ является параболой, а свободная поверхность жид­кости — параболоидом. Такую же форму имеют и другие поверх­ности уровня.

Пользуясь уравнением (1.34), можно определить положение свободной поверхности в сосуде, например максимальную вы­соту Н подъема жидкости и высоту h расположения вершины параболоида при данной угловой скорости w. Для этого необходимо использовать еще уравнение объемов: объем неподвижной жидкости равен ее объему во время вращения.

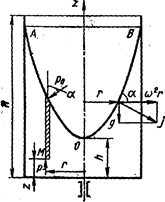
Рис. 1.18. Поверхность жидко­сти при вращении открытого cосуда вокруг вертикальной оси

Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты поступим аналогично тому, как это сделано в п. 1.5. Выделим вертикальный цилинд­рический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произволь­ном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (1.34) будем иметь

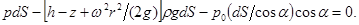
После сокращений получим

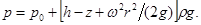(1.35)

Это значит, что давление возрастает пропорционально радиусу и уменьшается пропорционально высоте z.

Если сосуд, вращающийся вокруг вертикальной оси, имеет крыш­ку и заполнен жидкостью доверху, то ее форма измениться не может, но изменяется давление в соответствии с выражением (1.35). На рис. 1.19 показана эпюра давления по крышке, стенке и дну сосуда.

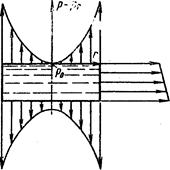Рис. 1.19. Эпюры давлений на крышку,

Дата добавления: 2014-01-05