Процесс оптимизации

Имеется задача. Для решения задачи нужно формализовать объект и представить его в виде математической модели.

Модели:

- физические;

- геометрические (фотография, рисунок);

- математические.

Математическая модель, та которая определена с помощью математических формализмов. Математическая модель не является точной, а является идеализацией. Модель характеризуется параметрами, которые могут быть и числовыми 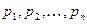. Их часть может характеризовать состояние объекта – параметры состояния , а другие могут относиться к процессу проектирования – переменные проектирования .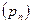

Определение параметров состояния - задача моделирования. Определение переменных проектирования – задачи проектирования или задачи оптимизации.

Допустим имеются 2 переменные 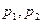. Задавая конкретные значения получаем точку.

G R – множество чисел

R

множество допустимых

вариантов

p₂ допустимое решение

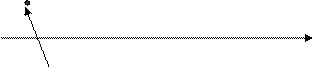p₁

недопустимое решение – не удовлетворяющее наложенным ограничениям

Плоскость множества возможных вариантов, на нее могут быть наложены ограничения.

Отображение множества 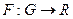- целевая функция позволяет формировать критерий для сравнения различных решений.

2 вида задач оптимизации:

- максимизации;

- минимизации.

Для оптимизационного решения задачи требуется:

1. Сформулировать задачу;
2. Построить математическую модель (определить множество переменных);
3. Определить ограничения на возможные решения;
4. Определить целевую функцию. Далее применим формальные математические методы, позволяющие найти решения.

Дата добавления: 2014-01-05