Обобщение

А

Методы для нахождения корня уравнения функции 1-ой переменной.

Деление пополам:

Имеется хотя бы 1 корень. Выбираем любую точку и смотрим какой знак она имеет, такой знак нам и искать. Выбираем точку приблизительно в середине интервала, исследуя значения в 3-х можно отбросить половину интервала.

+

b

-

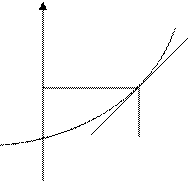
Метод Ньютона (метод касательной):

В случае если известна производная, то выбираем 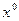- начальное приближение.

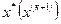
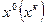
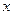
Допустим, что точка 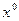достаточно близка к корню функции и примерно себя ведет линейно не отклоняется. Проведем касательную и находим точку ближе чем 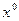, и повторяем до .

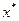Для метода Ньютона необходимо:

- функция должна иметь производную;

- точка должна быть взята близко к корню;

- функция изменяется близко к линейной функции.

;

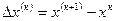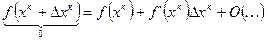- уравнение касательной;

.

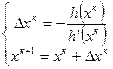Если 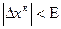, то вычисления можно прекратить и считать что нужный нам корень – условие прекращения поиска. (Е – значение корня с некоторой точностью).

В методе Ньютона каждя его итерация удваивает количество значащих цифр. Если все условия выполнены, то эти методы удваивают (ускоряют) количество значащих цифр:

;

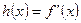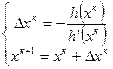
Представим что 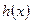линейная функция, то метод Ньютона позволяет найти ее корень за 1-у итерацию. Целевая функция представляет собой квадратичную зависимость следовательно метод Ньютона позволяет найти минимум или максимум квадратичной функции за 1-у итерацию.

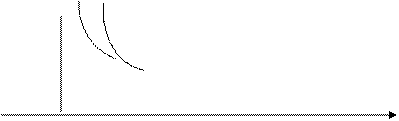
Замена функции на касательную, называется – линейная аппроксимация, и ее применение к целевой функции парабола в точке приближения.

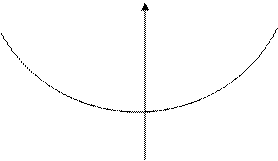f(x)

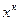х

Замена заданной зависимости квадратичной зависимостью, называется – квадратичной аппроксимацией. Метод Ньютона основан на замене заданной зависимости более простой зависимостью.

На практике часто необходимо найти экстремум (или экстремумы) некоторой целевой функции 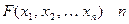переменных 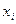(проектных параметров). Такая функция описывает 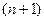- мерную поверхность. Соответственно функция 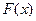одного параметра 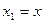описывает некоторую кривую на плоскости. Поиск экстремумов функции одной переменной является самостоятельной и часто встречающейся задачей.

Метод равномерного поиска основан на том, что переменной 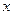присваиваются значения 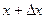с шагом 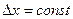и вычисляются значения 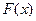. Если 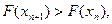переменной 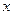даётся новое приращение. Как только 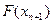станет меньше 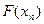, поиск останавливается. При малой заданной погрешности этот метод неэкономичен по затратам машинного времени.

Метод поразрядного приближения является разновидностью метода равномерного поиска и реализуется следующим алгоритмом.

1. Задаём начальное приближение 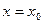слева от максимума 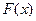и вычисляем 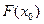. Задаём 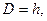где 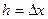- начальный шаг поиска.

2. Полагаем 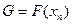, где вначале 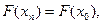задаём 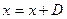и вычисляем .

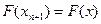3. Проверяем условие 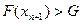; если оно выполняется, идём к п. 3, если нет – к п. 4.

4. Полагаем 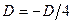. Проверяем услови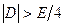е , где 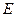- заданная погрешность вычисления 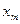в точке максимума. Если оно выполняется, идём к п. 2, т. е. обеспечиваем поиск максимума в другом направлении с шагом в 4 раза меньше прежнего. Если данное условие выполнятся, заканчиваем поиск.

Метод дихотомии (деления интервала поиска 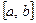пополам) реализуется следующим образом.

1. Проверяем услови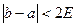е , где 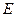- заданная погрешность вычисления 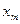. Если это условие выполняется, идём к п. 6; если не выполняется, идём к п. 2.

2. Делим интервал поиска 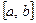пополам и вычисляем две абсциссы, симметрично расположенные относительно точки .

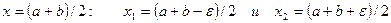3. Для этих значений 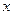вычисляем .

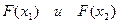4. Проверяем условие 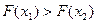. Если оно выполняется, полагаем 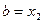и идём к п. 1. Если не выполняется, идём к п. 5.

5. Полагаем 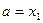и идём к п. 1.

6. Выводим на печать 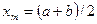и вычисляем .

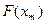Метод золотого сечения основан на делении отрезка 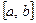по правилу золотого сечения. Он позволяет сужать отрезок 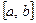, каждый раз вычисляя лишь одно значение 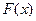, а не два, как в методе дихотомии. Данный метод реализуется следующим алгоритмом.

1. Находим коэффициент дробления 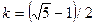отрезка .

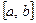2. Находим абсциссу 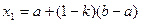и вычисляем .

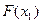3. Находим абсциссу 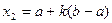и вычисляем .

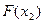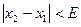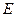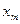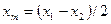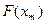4. Проверяем выполнение условия , где - заданная погрешность вычисления . Если это условие выполняется, вычисляем и , после чего останавливаем счёт с выдачей значени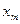й и 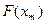. Если данное условие не выполняется, идём к п. 5.

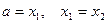5. Проверяем условие . Если оно выполняется, полагаем и 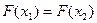, после чего выполняем п.3 и п. 4.

6. Если 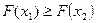, полагаем ,,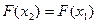 после чего выполняем п. 2.

Дата добавления: 2014-01-05