
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Евклидово пространство
|
|
|
|
Определение 7. Скалярным произведением двух векторов  и
и 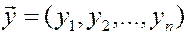 пространства
пространства  называется число, определяемое по формуле:
называется число, определяемое по формуле:
 . (5)
. (5)
Скалярное произведение имеет экономический смысл. Если  есть вектор объемов различных товаров,
есть вектор объемов различных товаров, 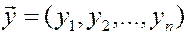 вектор их цен, то скалярное произведение
вектор их цен, то скалярное произведение 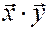 выражает суммарную стоимость этих товаров.
выражает суммарную стоимость этих товаров.
Скалярное произведение обладает следующими свойствами:
1) 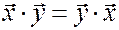 - коммутативность;
- коммутативность;
2) 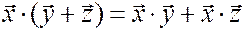 - дистрибутивность;
- дистрибутивность;
3) 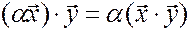 , где
, где 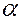 - любое действительное число;
- любое действительное число;
4)  , если
, если  ;
;  , если
, если  .
.
Определение 8. Векторное пространство, в котором определена операция - скалярное произведение векторов, удовлетворяющая четырем вышеперечисленным свойствам, называемых аксиомами, называется евклидовым пространством.
Определение 9. Длиной (нормой) вектора 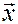 в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
в евклидовом пространстве называется корень квадратный из его скалярного квадрата:
 ,
,
где  - координаты вектора
- координаты вектора 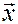 .
.
Угол между двумя векторами 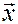 и
и 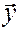 определяется по формуле:
определяется по формуле:
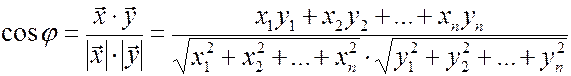 ,
,
где  .
.
Определение 10. Два вектора  и
и 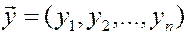 из
из  называются ортогональными, если их скалярное произведение равно нулю
называются ортогональными, если их скалярное произведение равно нулю  , т.е.
, т.е.
 .
.
Определение 11. Нормированием вектора  называется отношение:
называется отношение:  . В результате получается вектор, длина которого равна 1, а направление его совпадает с направлением вектора
. В результате получается вектор, длина которого равна 1, а направление его совпадает с направлением вектора 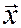 .
.
Определение 12. Ортонормированным базисом пространства 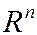 называется система векторов
называется система векторов 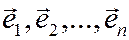 , которые попарно ортогональны, т.е.
, которые попарно ортогональны, т.е. 
 , а длина каждого равна единице, т.е.
, а длина каждого равна единице, т.е. 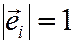 ,
,  .
.
Теорема 2. Во всяком 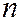 - мерном евклидовом пространстве существует ортонормированный базис.
- мерном евклидовом пространстве существует ортонормированный базис.
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 510; Нарушение авторских прав?; Мы поможем в написании вашей работы!