Размерность и базис векторного пространства

Определение 3. Вектор 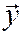называется линейной комбинацией векторов , ,…, векторного пространства , если , где 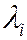() - любые действительные числа.

Определение 4. Векторы , ,…, векторного пространства называются линейно зависимыми, если существуют такие числа 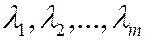, не равные одновременно нулю, что . Если же эта нулевая линейная комбинация имеет место только тогда, когда все (), то система векторов называется линейно независимой.

Определение 5. Векторное пространство называется 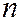-мерным, если в нем существует 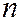линейно независимых векторов, а любые из векторов уже являются зависимыми.

Таким образом, размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Число 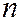называется размерностью пространства. Векторное пространство размерности 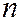обозначают .

Определение 6. Совокупность из 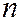линейно независимых векторов пространства называется базисом этого пространства.

Пространство может иметь несколько различных базисов.

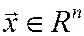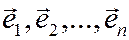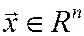Теорема 1. Каждый вектор можно представить единственным образом в виде линейной комбинации векторов базиса. Если - базис пространства и , то .

Это равенство называют разложением вектора 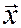по базису 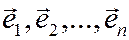, а числа - координатами вектора 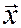в этом базисе.

3. Переход к новому базису. Пусть в пространстве заданы два базиса: старый 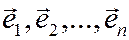и новый . На основании предыдущей теоремы каждый из векторов нового базиса можно представить в виде линейной комбинации векторов старого базиса:

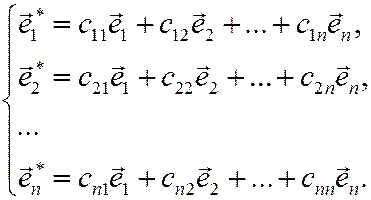(1)

Полученная система означает, что переход от старого базиса 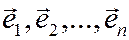к новому задается матрицей перехода:

, (2)

причем коэффициенты разложения новых базисных векторов по старому базису образуют столбцы этой матрицы.

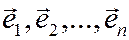Матрица - невырожденная (), так как в противном случае ее столбцы (а следовательно, и базисные векторы) оказались бы линейно зависимыми. Обратный переход от нового базиса к старому базису осуществляется с помощью обратной матрицы .

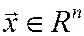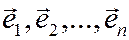Найдем зависимость между координатами вектора в разных базисах. Пусть , причем в базисе и 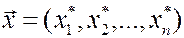в базисе , т.е.

. (3)

Подставив значения из системы (1) в левую часть равенства (3), получим после преобразований:

т.е. в матричной форме

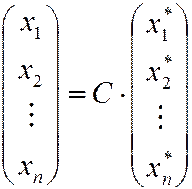или . (4)

Пример 1. Найти координаты вектора 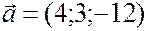в базисе, образованном векторами , , .

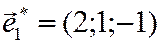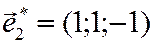Решение. Выразим связь между базисами:

Матрица перехода от базиса к базису 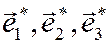имеет вид

.

Найдем .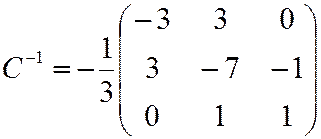

Теперь по формуле (4)

,

т.е. новые координаты вектора в базисе 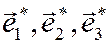и вектор может быть представлен в виде:

.

Дата добавления: 2014-01-05