
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теорема о целочисленности решения КТЗ
|
|
|
|
Если в КТЗ (1)-(4) значения 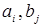
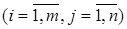 целые, то и оптимальный план КТЗ будет целочисленным.
целые, то и оптимальный план КТЗ будет целочисленным.
Доказательство. Пусть 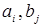 - целые числа и КТЗ решена методом потенциалов. Начальный опорный план такой задачи будет целочисленным, так как при его построении в каждой клетке назначалась целочисленная переменная
- целые числа и КТЗ решена методом потенциалов. Начальный опорный план такой задачи будет целочисленным, так как при его построении в каждой клетке назначалась целочисленная переменная 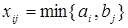 . При переходе к лучшему опорному плану вычислялась добавка Q=min{
. При переходе к лучшему опорному плану вычислялась добавка Q=min{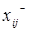 }, поэтому Q также будет целым. Это целое число либо прибавляется к компонентам опорного плана, либо вычитается из них. Т.о. все рассматриваемые в ходе решения задачи опорные планы будут целочисленными. Следовательно, и оптимальный план будет целочисленным. Ñ
}, поэтому Q также будет целым. Это целое число либо прибавляется к компонентам опорного плана, либо вычитается из них. Т.о. все рассматриваемые в ходе решения задачи опорные планы будут целочисленными. Следовательно, и оптимальный план будет целочисленным. Ñ
Задача о назначениях.
(Задача выбора)
Постановка задачи. Пусть имеется n заказов с номерами 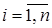 и имеются n исполнителей с номерами
и имеются n исполнителей с номерами 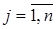 , т.е. число заказов равно числу исполнителей. Любой заказ м.б. выполнен любым исполнителем., при этом стоимость выполнения i –того заказа j -тым исполнителем равна
, т.е. число заказов равно числу исполнителей. Любой заказ м.б. выполнен любым исполнителем., при этом стоимость выполнения i –того заказа j -тым исполнителем равна 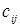 . Необходимо закрепить заказы за исполнителями так, чтобы все заказы были выполнены, у всех исполнителей был заказ, а суммарная стоимость выполнения заказов была бы минимальной.
. Необходимо закрепить заказы за исполнителями так, чтобы все заказы были выполнены, у всех исполнителей был заказ, а суммарная стоимость выполнения заказов была бы минимальной.
Построим ММ задачи.
Пусть 
Тогда модель задачи о назначениях запишется в виде:
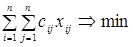 (1)
(1)
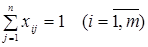 (2)
(2)
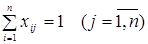 (3)
(3)
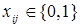 (4)
(4)
Здесь целевая функция (1) выражает суммарную стоимость выполнения заказов, ограничения (2) требуют, чтобы у каждого заказа был исполнитель, а ограничения (3) – чтобы у каждого исполнителя был заказ.
Модель (1)-(4) относится к классу задач линейного целочисленного, а именно булевского, программирования. Решение такого класса задач является очень трудоемким и за приемлемое время можно получить решение лишь для задач небольшой размерности. Однако задача (1)-(4) имеет особенности, которые позволяют свести ее к КТЗ. Для этого условие (4) записывается условно как:
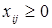 (5).
(5).
Тогда задача (1)-(3), (5) является частным случаем КТЗ при m=n, 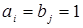 . Пусть эта задача решена методом потенциалов и получено решение
. Пусть эта задача решена методом потенциалов и получено решение 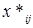 . Будет ли это решение являться и решением исходной задачи (1)-(4)? ДА! На основании теоремы о целочисленности решения КТЗ значения
. Будет ли это решение являться и решением исходной задачи (1)-(4)? ДА! На основании теоремы о целочисленности решения КТЗ значения 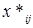 целые. Они удовлетворяют ограничениям (2), (3). Но сумма неотрицательных целых чисел очевидно будет равна 1 только тогда, когда слагаемые равны 0 и 1, т.е.
целые. Они удовлетворяют ограничениям (2), (3). Но сумма неотрицательных целых чисел очевидно будет равна 1 только тогда, когда слагаемые равны 0 и 1, т.е. 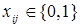 . Таким образом выполняется условие (4).
. Таким образом выполняется условие (4).
Если число заказов больше или меньше числа исполнителей, то вводят либо фиктивных исполнителей, либо фиктивные заказы.
Примечание. Таким образом, задачу о назначениях можно решить как КТЗ. Однако существуют специальные более эффективные методы. Один из таких алгоритмов известен под названием «Венгерский метод» (см. Таха Х. «Введение в ТПР»).
Транспортная задача в сетевой постановке
(с промежуточными пунктами).
В КТЗ продукция перевозится непосредственно из любого пункта производства в любой пункт потребления. Однако в реальных задачах перевозка грузов производится по различным коммуникациям. Из данного пункта производства в данный пункт потребления можно попасть различными путями, побывав в других промежуточных пунктах. Например: Заводы- Оптовые базы- Потребители.
 Постановка задачи. Пусть дана транспортная сеть, т. е. совокупность множества узлов и направленных дуг, соединяющих эти узлы между собой. Узлы сети пронумерованы как
Постановка задачи. Пусть дана транспортная сеть, т. е. совокупность множества узлов и направленных дуг, соединяющих эти узлы между собой. Узлы сети пронумерованы как 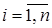 , каждый узел сети означает некоторый пункт. Если узел i соединен с узлом j дугой (i,j), то это означает возможность непосредственного движения из пункта i в пункт j. Каждый узел i взвешен числом
, каждый узел сети означает некоторый пункт. Если узел i соединен с узлом j дугой (i,j), то это означает возможность непосредственного движения из пункта i в пункт j. Каждый узел i взвешен числом  , означающим объем продукции в этом пункте. Если
, означающим объем продукции в этом пункте. Если 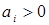 , то в этом пункте имеется излишек продукции, а если
, то в этом пункте имеется излишек продукции, а если 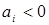 , то недостаток продукции в количестве
, то недостаток продукции в количестве  . Если же
. Если же 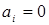 , то в этом пункте нет ни излишка, ни недостатка. Будем считать, что
, то в этом пункте нет ни излишка, ни недостатка. Будем считать, что 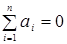 , т.е. суммарный излишек продукции равен суммарной потребности. Каждая дуга (i,j) взвешена числом
, т.е. суммарный излишек продукции равен суммарной потребности. Каждая дуга (i,j) взвешена числом 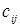 - стоимостью перевозки единицы продукции по дуге (i,j). В общем случае
- стоимостью перевозки единицы продукции по дуге (i,j). В общем случае 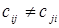 . В транспортной сети присутствуют дуги в виде петель.
. В транспортной сети присутствуют дуги в виде петель.
Требуется найти такой план перевозок из пунктов с излишками в пункты с недостатками, чтобы суммарная стоимость перевозок была наименьшей.
В настоящее время для решения таких задач существуют достаточно эффективные алгоритмы, основанные на модификации метода последовательного улучшения плана ЗЛП.
Рассмотрим два способа решения транспортной задачи в сетевой постановке, основанные на ее сведении к КТЗ: метод отыскания путей минимальной стоимости и метод буферного запаса.
|
|
|
|
|
Дата добавления: 2014-01-05; Просмотров: 414; Нарушение авторских прав?; Мы поможем в написании вашей работы!