Виды волн

Тип механических волн существенно определяется характеристиками сред, в которых они распространяются.

Газы и жидкости не оказывают упругого сопротивления сдвигу слоев. Попытка же сжать или расширить какой-либо объем сопровождается возникновением сил упругости. Отсюда следует, что в жидкостях и газах возможны только волны, направление распространения которых совпадает с направлением возмущения параметров среды. Такие волны называются продольными:

.

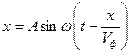Типичным примером продольной волны является звуковая волна.

В твердом теле, в отличие от жидкостей и газов, возможна деформация вида «сдвиг», вследствие этого направление распространения волны может не совпадать с направлением возмущения параметров среды. Если направление распространения волны и направление возмущения параметров среды ортогональны, то такая волна является поперечной.

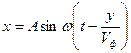
Характерным примером такого типа волны является волна изгиба.

В твердых телах возможно распространение продольных, поперечных и косых волн. Примером косой волны является волна «вздутия», возникающая при резком ударе по торцу длинного стержня, когда продольная деформация приводит к деформации поперечной (коэффициент Пуассона).

Широко распространенным типом волн являются поверхностные волны – волны, возникающие на границе раздела двух сред, например, жидкости и газа. В поверхностной волне частицы среды описывают эллиптические траектории.

3.11. Фазовая и групповая скорости распространения волн. Дисперсия. Формула Рэлея.

Фазовая скорость распространения волн (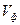) зависит от упругих свойств среды.:

-для продольных волн ,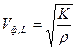

где 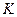- модуль объемной упругости среды, 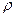- ее плотность,

- для поперечных волн ,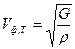

где 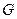- модуль сдвига,

- для поверхностных волн, возникающих на границе раздела жидкость – газ ,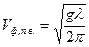

где 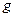- ускорение свободного падения,

- для капиллярных (коротковолновые волны) волны на поверхности жидкости

,

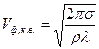где 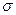- коэффициент поверхностного натяжения.

Видим, что в ряде случаев фазовая скорость распространения волны зависит от длины волны. Такая зависимость называется дисперсией.

Ранее отмечалось, что волновой процесс, это процесс переноса в пространстве энергии путем передачи импульса от одного слоя среды к другому. Казалось бы, энергия переносится с фазовой скоростью распространения волны. Это действительно так, если мы имеем дело с монохроматической волной или если нет дисперсии.

Ситуация меняется, есть распространяется группа волн с различными частотами и есть дисперсия. В этом случае скорость распространения энергии будет определяться скоростью распространения центра энергии группы волн, которая называется групповой скоростью ( 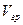). Центр энергии группы волн возникает в области пространства, в которой фазы волн, составляющих рассматриваемую группу, соответствуют их максимальным амплитудам. Центр энергии возникает в результате интерференции волн составляющих рассматриваемую группу.

Найдем скорость движения центра энергии группы волн.

Пусть в момент времени 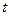центр энергии группы волн находится в точке «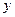». В этой точке фазы всех волн, составляющих рассматриваемую группу,

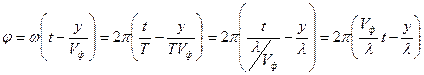
совпадают и не зависят от длины волны

.

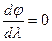Поэтому можно записать выражение:

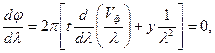
из которого следует:

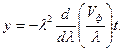
Видим, что множитель 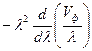в полученном выражении является скоростью, а в соответствии с поставленной задачей - групповой скоростью

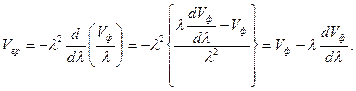
Соотношение

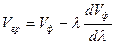
называется формулой Рэлея.

Видно, что если дисперсия отсутствует (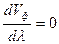), то групповая скорость равна фазовой. Если 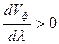, то групповая скорость меньше фазовой – нормальная дисперсия, если 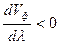, то 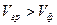и дисперсия называется аномальной.

Дата добавления: 2014-01-05