Тема 3. Рисунок 7– Модель и эпюр точки А в системе V, Н, W

В

А б

Б в

А

А б в

А б в

А б

А б в

Рисунок 7 – Модель и эпюр точки А в системе V, Н, W

Появление на эпюре оси Y₁ объясняется тем, что ось Y при совмещении плоскостей проекций Н и W с плоскостью V как бы раздвоилась — одна ее часть ушла вниз с плоскостью Н (на эпюре она обозначена буквой Y), а вторая — вправо с плоскостью W (на эпюре она обозна­чена буквой Y₁).

На эпюре фронтальная и профильная проек­ции точки лежат на одной линии связи, которая перпендикулярна к оси проекций Z, причем профильная проекция точки находится на та­ком же расстоянии от оси Z, как и горизонталь­ная от оси X.

Прямые линии, соединяющие проекции точки и перпендикулярные осям проекций, называют линиями связи (рис. 7б, в).

Поскольку две проекции точки определяют ее положение в пространстве, то по двум проекциям можно построить третью, которая оказывается необходимой в тех случаях, когда проекционный чертеж объекта сложен и требуются дополнительные данные для прочтения формы объекта.

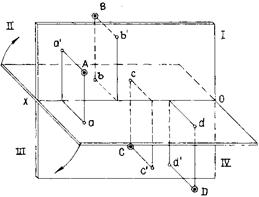
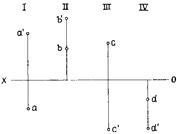
Рисунок 8 – Положение проекций точек в зависимости от четверти пространства, в которой расположены точки

Если профильная плоскость проек­ций W не используется, плоскости Н и V разделяют пространство на четыре двугранных угла — четверти (рис. 8 а). Ось проекций разделяет плоскости проекций на две полуплоскости.

Положение проекций точек на эпю­ре (рис. 8 б) зависит от того, в какой четверти пространства расположена точка. Точка В расположена во второй четверти, ее проекции на эпюре нахо­дятся над осью Х. Горизонтальная про­екция точки С, расположенной в третьей четверти, после совмещения плоскостей окажется над осью, а фрон­тальная проекция — ниже оси. Обе проекции точки D, расположенной в четвертой четверти, находятся ниже оси Х. Две проекции точки могут совпадать (во второй и четвертой четвертях) или находиться на одинаковом расстоянии от оси проекций (в первой и третьей четвертях), если их координаты одина­ковы.

Знаки координат в каждом из октантов указаны в табл. 1.

Точка в пространстве может быть определена не только ее проекциями, но и прямоугольными (декартовыми) координатами.

Известно, что координаты какой-либо точ­ки — это числа, выражающие ее расстояния от трех взаимно перпендикулярных плоскостей, называемых плоскостями координат.

Таблица 1 – Знаки прямоугольных координат

в различных четвертях и октантах

Номер четверти или октанта	X	Y	Z
Ι	+	+	+
ΙΙ	+	-	+
ΙΙΙ	+	-	-
ΙV	+	+	-

На рис.9 построена в проекциях точка А по ее координатам х, у, z, где х — абсцисса; у — ордината; z — аппликата.

Приняв оси и плоскости координат за оси и плоскости проекций, легко заметить, что аб­сцисса точки (х) — это расстояние ее от плос­кости проекций W, координата (у) — расстояние от плоскости проекций V и аппликата (z) — расстояние от плоскости проекций Н.

Как видно из приведен­ного изображения, каждая проекция точки определяется двумя координатами: фронталь­ная — абсциссой х и аппликатой z, горизон­тальная — абсциссой х и ординатой у, профиль­ная — ординатой у и аппликатой z. Следова­тельно, по координатам точки может быть по­строен и ее эпюр.

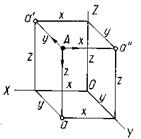
Рисунок 9 - Построение в проекциях точки А по ее координатам х, у, z

Проекции прямой линии оп­ределяются проекциями двух точек, принадлежащих этой ли­нии, прямая на эпюре задается двумя проекциями.

На рис.10 приведен эпюр от­резка АВ в системе V, Н, W. Отрезок АВ не параллелен ни одной из плоскостей проекций – это отрезок прямой общего положения. У отрезка прямой общего по­ложения:

а'b' < АВ;

ab < AB;

а"b" < АВ,

т.е. каждая его проекция меньше истинной величины самого отрезка.

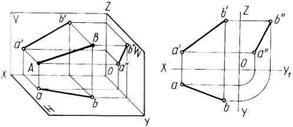
Рисунок 10 – Прямая общего положения

В отличие от прямых общего положения прямые параллельные или перпендикулярные плоскостям проекций, называются прямыми частного положения. Прямые, параллельные одной из плоскостей проекций, называют линиями уровня (рис. 11).

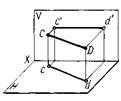
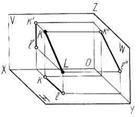
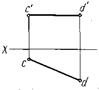
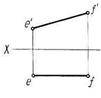
Рисунок 11 – Модели и эпюры прямых уровня: а – горизонтали, б – фронтали, в - профильной прямой

Отрезок прямой CD (рис. 11а) параллелен плоскости проекций Н – это горизонтальная прямая. У отрезка горизонтальной прямой cd = CD.

Отрезок прямой EF (рис. 11б) параллелен плоскости проекций V – это фронтальная пря­мая. У отрезка фронтальной прямой e'f'—EF.

Отрезок прямой KL (рис. 11в) параллелен плоскости проекций W – это профильная пря­мая. У отрезка профильной прямой k"l" = KL.

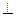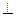Прямые, перпендикулярные плоскостям проекций, называют проецирующими (рис. 12): АВН, CD V, EF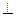W, АВ — горизонтально проецирующая, CD — фронтально проецирующая, EF — профильно проеци­рующая прямая.

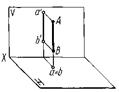
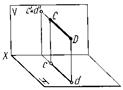
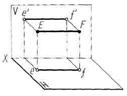
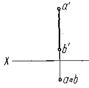
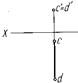
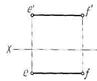
Рисунок 12 – Модели и эпюры проецирующих прямых: а – горизонтально проецирующей, б – фронтально проецирующей, в – профильно проецирующей прямой

Длину отрез­ка прямой можно определить по двум его проекциям из прямоугольного треу­гольника аbА₀ (рис. 13 а, б), в котором одним катетом является горизонталь­ная проекция ab отрезка, а другим — разность координат его кон­цов (∆z), взятая из другой проекции. Ги­потенуза А₀b прямоугольного треуголь­ника есть длина отрезка. Угол α в этом треугольнике определяет угол наклона прямой к плоскости Н. Длину отрезка прямой можно определить аналогич­но, построив прямоугольный треугольник на фронтальной проекции отрезка (рис. 13б). Угол β в этом треугольнике определяет наклон прямой АВ к плоскости V.

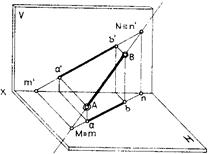
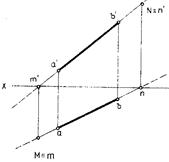
Следами пря­мой называются точки пересечения прямой с плоскостями проекций (рис. 14а): М(т;т') — горизонтальный след прямой; N(n;n') — фронтальный след. На рис. 14б дан эпюр прямой АВ, а также горизонтальный и фронтальный следы прямой.

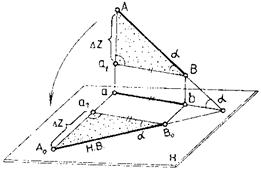
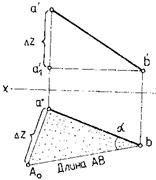
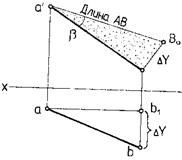
Рисунок 13 – Определение длины отрезка прямой способом прямоугольного треугольника

Для определения на эпюре горизон­тального следа прямой необходимо продолжить ее фронтальную проек­цию до пересечения с осью Ох и в этой точке восставить перпендикуляр до пересечения с горизонтальной проекцией прямой. Фронтальный след пря­мой определяют аналогично.

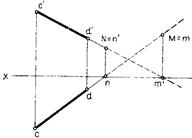
Следы прямой строятся как точки пересечения прямой со своими проек­циями, поэтому каждый след совпадает со своей одноименной проекцией. Сле­ды прямой являются точками, в кото­рых прямая переходит из одной четвер­ти в другую. Так, прямая АВ (рис. 14 а, б) проходит через I, II и IV четверти пространства. Прямая CD (рис. 14 в) — через I, II и III четверти. Видимой час­тью прямой будет та ее часть, которая расположена в первой четверти.

Рисунок 14 –Модель и эпюры построения следов прямых

Дата добавления: 2014-01-05