Тема 6. Рисунок 39 –Преобразование прямой общего положения в прямую уровня способом замены плоскостей проекций

А б

А б

А б

А б

Б в

Рисунок 39 – Преобразование прямой общего положения в прямую уровня способом замены плоскостей проекций

При замене плоскостей проекций расстояние от новой проекции точки до новой оси равно расстоянию от за­меняемой проекции точки до старой оси проекций. Иными словами, высоты (аппликаты) концов отрезка в новой си­стеме плоскостей проекций останутся прежними. В результате этой замены определены действительная величина отрезка прямой и угол наклона α к пло­скости Н. При переходе к эпюру пло­скость V₁ совмещается с плоскостью Н.

Второе преобразование (рис. 39в). Для того чтобы прямая АВ оказалась про­ецирующей, т. е. изобразилась точкой, необходимо произвести вторую замену плоскости проекций и расположить но­вую плоскость Н₁ перпендикулярно прямой. Новая ось х₂ выбрана на эпюре перпендикулярной новой фронтальной проекции прямой а₁'b'₁. На новой пло­скости проекций Н₁, прямая изобразится точкой, так как координаты концов от­резка в системе Н₁/V₁ одинаковы.

Таким образом, прямая АВ в систе­ме Н₁/V₁ стала проецирующей относи­тельно плоскости Н_1. Преобразования в этой задаче могли быть выполнены и в другой последовательности: сначала могла быть заменена горизонтальная плоскость проекций, а затем — фрон­тальная.

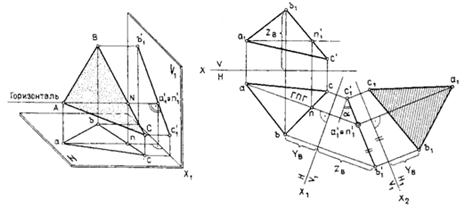
Рисунок 40 – Определение истиной величины плоской фигуры общего положения способом замены плоскостей проекций:

а – модель; б – эпюр

Рассмотрим еще одну задачу:требуется определить истинную ве­личину плоской фигуры — треугольни­ка АВС, занимающего в пространстве общее положение. Для решения этой за­дачи необходимо преобразовать эпюр так, чтобы плоскость общего положе­ния стала параллельной одной из пло­скостей проекций новой системы. В ор­тогонально-проекционной системе ре­шить эту задачу одной заменой плоско­сти проекций нельзя. Как и в предыду­щей задаче, необходимо выполнить два преобразования, но в иной последовательности: сначала следует преобразо­вать плоскость общего положения в проецирующую, а затем — в плоско­сть уровня.

На рис. 40а сначала заменена фронтальная плоскость проекций но­вой плоскостью V₁, перпендикулярной плоскости треугольника. Это условие выполнено с помощью вспомогатель­ной прямой — линии уровня, например, горизонтали AN ( рис. 40б). Новая ось х₁ проведена на эпюре перпендикуляр­но горизонтальной проекции горизон­тали. На новой плоскости проекций V₁ горизонталь спроецировалась в точку, а плоскость треугольника — в линию.

Угол α определяет угол наклона треу­гольника к горизонтальной плоскости Н.

На втором этапе решения проведе­на вторая замена — новая плоскость проекций Н₁ установлена параллельно треугольнику. Новая ось х₂ проведена параллельно новой фронтальной проек­ции треугольника — прямой a'₁b'₁c'₁. Построенная проекция определяет истин­ную величину и форму треугольника.

Если плоскость задана следами, а не плоской фигурой, ее следует преобра­зовать в проецирующую (рис. 41). Для этого но­вую плоскость проекций и новую ось проекций следует расположить перпен­дикулярно, например, к горизонтально­му следу заданной плоскости, при этом горизонтальный след спроецируется на новой плоскости в точку (Р_х1).

Для построения новой проекции фрон­тального следа Р_у1 достаточно найти проекцию любой точки заданной пло­скости, например произвольной точки N, лежащей на следе. Прямая Р_х1 — n'₁ является искомым проецирующим сле­дом данной плоскости.

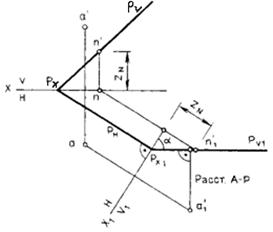
Рисунок 41 – Преобразование плоскости общего положения, заданной следами в проецирующую, способом замены плоскостей проекций

Способ вращения. Сущность способа вращения состоит в изменении положения объек­та, заданного на эпюре, таким образом, чтобы определенные его элементы за­няли относительно плоскостей проек­ции частное положение и проецирова­лись без искажения.

Вращение может производиться вокруг осей, расположенных относи­тельно плоскостей проекций различ­ным образом. Ниже рассматриваются следующие разновидности способа вра­щения: вращение вокруг проецирую­щих осей, вращение вокруг линий уровня и совмещение.

а б

Рисунок 42 – Вращение вокруг проецирующих осей:

а -модель, б – эпюр

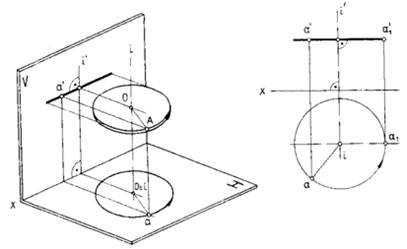
Вращение вокруг проецирующих осей. При вращении точки вокруг оси, перпендикулярной плоскости проек­ций, одна ее проекция перемещается по окружности, а вторая — по прямой, перпендикулярной проекции оси вра­щения (рис. 42а).

Окружность, описы­ваемая точкой А, спроецируется на пло­скости Н без искажения, а на плоскости V — в виде отрезка прямой. При враще­нии точки вокруг фронтально проеци­рующей оси ее траектория проецирует­ся на фронтальную плоскость проекций окружностью, а на горизонтальную плоскость — отрезком прямой, перпен­дикулярным проекции оси.

В процессе решения задач способом вращения вокруг проецирующих осей этапы преобразований геометрических элементов аналогичны тем, которые выполнялись способом замены плоско­стей проекций.

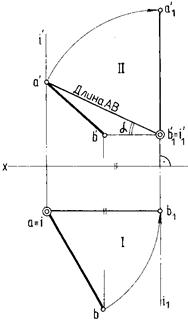
На рис. 44 прямая общего положе­ния одним вращением вокруг горизон­тально проецирующей оси i преобразо­вана в линию уровня (фронталь), а за­тем вторым вращением вокруг оси i₁, перпендикулярной фронтальной проек­ции, приведена в проецирующее поло­жение — проецируется на плоскость Н в точку.

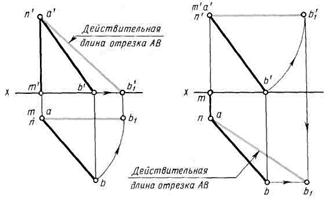
Рисунок 43 -Определение натуральных величин прямых общего положения способом вращения

Преобразования, аналогичные тем, которые выполнялись способом замены плоскостей проекций, производятся и при определении вращением действи­тельной величины плоской фигуры.

Двойное вращение вокруг проеци­рующих осей приводит обычно к тому, что последующие построения и новая проекция объекта накладываются на заданную проекцию, что затрудняет чтение эпюра. Поэтому способ вращения вокруг проецирующих осей целесообразно применять при решении задач одним вращением.

Вращение вокруг линий уровня. Этот способ применяется для преобразования плоскости общего положения плоскость уровня и для определения действительной величины плоской фигуры. Задача решается одним вращением вокруг линии уровня данной плоскости – горизонтали или фронтали.

На рис. 45а показано вращение некоторой точки А вокруг горизонтальной прямой МN до тех пор, пока точка А не окажется в плоскости, параллельной плоскости проекций Н и определяемой этой точкой и осью вращения.

При вращении вокруг горизонтальной прямой МN точка А перемещается по дуге радиуса ОА, лежащей в плоскости Q, перпендикулярной к оси вращения. когда точка А займет нужное положение А₁, горизонтальная проекция радиуса вращения (оа₁) будет равна его истинной величине, которая может быть определена способом прямоугольного треугольника. На рис. 45б эти же построения выполнены на эпюре.

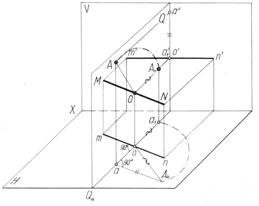
Рисунок 45 – Вращение точки вокруг горизонтальной прямой:

а -модель, б – эпюр

На рис. 46 в плоскости, заданной треугольником АВС, проведена горизонталь через вершину А и точку D на продолжении противоположной стороны треугольника. Горизонталь принята за ось вращения. Точки А и D при вращении останутся неподвижными. Вершины В и С вращаются по окружностям, которые проецируются на горизонтальной проекции отрезками прямых, перпендикулярными проекции оси. Так как треугольник должен занять горизонтальное положение, радиус вращения вершины В, например, должен проецироваться в натуральную величину. Длину радиуса R_B можно определить способом прямоугольного треугольника. Определив горизонтальное положение радиуса вращения вершины В, построим вершину С₁ в пересечении прямой b₁d с проекцией ее траектории вращения. Полученная проекция ab₁c₁ и определяет истинную величину треугольника.

Совмещение — частный случай вращения вокруг горизонтали или фронтали, когда осью вращения является горизонтальный или фрон­тальный след плоскости. При вращении пло­скости вокруг ее горизонтального или фрон­тального следа до совмещения с соответствую­щей плоскостью проекций лежащая в этой пло­скости фигура спроецируется на плоскость проекций в натуральную величину.

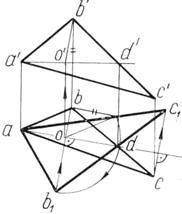
Рисунок 46 – Вращение треугольника вокруг горизонтальной прямой

Чтобы найти истинную величину плоской фи­гуры способом совмещения, надо совместить с одной из плоскостей проекций ряд характерных точек ее периметра.

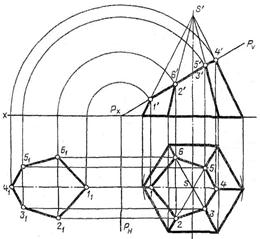
Рисунок 47 – Определение натуральной величины сечения способом совмещения

На рис. 48а показано совмещение некоторой плоскости Р с плоскостью проекций Н. Так как горизонтальный след плоскости Р (Р_Н) – ось вращения, то его положение и положение точки Р_Х не меняется. Для нахождения Р_V в совмещенном положении (Р_1V) на нем взята произвольная точка N и найдено новое положение ее, совмещенное с плоскостью проекций Н (N₁). Точка N при вращении вокруг Р_Н перемещается в плоскости Q, перпендикулярной к Р_Н, по дуге радиуса ОN, и совмещенное положение ее (N₁) определяется пересечение этой дуги с Q_Н. Фронтальный след плоскости в совмещенном положении (Р_1V) проведен через точки Р_Х и N₁. При этом отрезок ОN₁ является истинной величиной радиуса вращения.

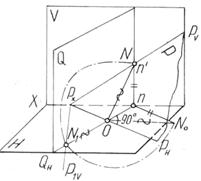
На рис. 48б эти построения выполнены на эпюре. Истинная величина радиуса вращения найдена способом прямоугольного треугольника. Однако практически определять истинную величину радиуса вращения точки N нет необходимости, так как отрезок Р_Хn^/ равен отрезку Р_ХN₁. Поэтому для нахождения точки N₁ достаточно провести дугу радиуса Р_Хn^/ до пересечения с Р_Н.

Рисунок 48 – Совмещение плоскости Р с плоскостью проекций Н:

а -модель, б – эпюр

На рис. 49а выполнено совмещение заданной плоскости Р и лежащей в ней некоторой точки А с плоскостью проекций Н. Для этого вначале найдено совмещенное с плоскостью Н положение горизонтали АN (а₁n₁), на которой находится точка А, и на ней отмечена точка а₁.

На рис. 49б плоскость Q и лежащая в ней точка В совмещены с плоскостью проекций V.

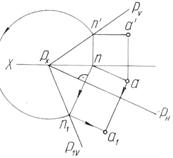
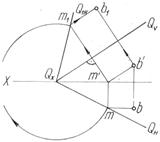
Рисунок 49 – Совмещение плоскости с плоскостью проекций:

а - Н, б – V

Способ плоскопараллельного пере­мещения. Плоскопараллельное перемещение можно рассматривать как вращение вокруг невыявленных проецирующих прямых. При плоскопараллельном перемещении геометрического образа одна из его проекций (оставаясь равной самой себе) перемещается в плоскости проекций, другие проекции точек геометрического образа перемещаются по прямым, параллельным направлению оси проекций (рис. 50).

Рисунок 50 – Определение натуральной величины прямой

способом плоскопараллельного перемещения

На рис. 51 плоскость треугольника общего положения двумя последова­тельно проведенными перемещениями приведена в положение, параллельное плоскости Н. Первое перемещение (Ι) выполнено с помощью вспомогатель­ной линии уровня — горизонтали. Тре­угольник приведен во фронтально-про­ецирующее положение. Вторым пере­мещением (II) плоскость приведена в горизонтальное положение. Новую проекцию располагают на свободном поле эпюра. Перемещение проводится параллельно плоскостям проекций, по­этому изображения вершин треуголь­ника на второй проекции перемещают­ся по прямым, перпендикулярным ли­ниям связи.

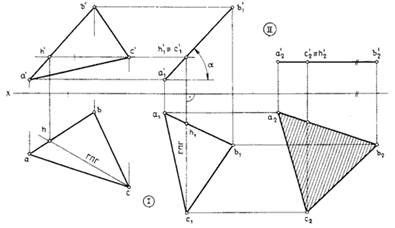
Рисунок 51 – Определение натуральной величины треугольника

способом плоскопараллельного перемещения

Дата добавления: 2014-01-05