Построение касательной к кривой поверхности. Пересечение кривых поверхностей плоскостью и прямой линией. Взаимное пересечение поверхностей. Метод сфер

КРИВЫЕ ЛИНИИ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ. КРИВЫЕ ПОВЕРХНОСТИ.

Кривые линии в начертательной геометрии рассматриваются как не­прерывная совокупность последова­тельных положений движущейся точ­ки, а также как линия пересечения по­верхностей.

Кривые ли­нии могут быть плоскими и про­странственными (линиями дво­якой кривизны). Если все точки кривой ли­нии лежат в одной плоскости, то такая кривая называется плоской. Примером могут служить окружность, эллипс, па­рабола. Если кривая не лежит всеми своими точками в плоскости, то она на­зывается пространственной, напри­мер винтовые линии. Кривые линии подразделяются и по другим призна­кам.

Кривая может быть зада­на аналитически, т. е. уравнением, например эллипс, парабола и др. Если образование кривой не имеет строгой закономерности, то она задается графи­чески, например горизонтали на плане местности, т.е. имеет случайный вид.

Степень уравнения, которое выра­жает алгебраическую кривую, опреде­ляет порядок кривой. Геометрически порядок плоской кривой определяется числом точек ее пересечения прямой линией (как действительных, так и мни­мых точек). Порядок пространственной кривой определяется числом точек пе­ресечения кривой с плоскостью.

В начертательной геометрии кри­вые линии изучаются по их проекциям.

Для того чтобы получить проекцию кривой линии, надо спроецировать на плоскость проек­ций ряд принадлежащих ей точек, а для опре­деления длины какого-либо участка ее надо вписать в эту кривую ломаную линию и опре­делить длину каждого ее звена.

Плоские кривые. Наиболее распространенными являются плоские кривые линии. Для исследования локальных свойств пло­ской кривой строят в некоторой точке касательную и нормаль.

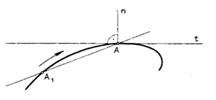
Касательной к плоской кривой в некоторой ее точке называется пре­дельное положение секущей, когда две общие с кривой точки сечения, стремясь друг к другу, совпадут (рис. 62а). Каса­тельная определяет направление дви­жения точки по кривой.

а

Нормалью называется прямая, ле­жащая в плоскости кривой и перпенди­кулярная касательной в точке ее каса­ния.

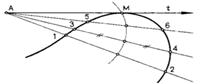
При решении некоторых задач при­ходится проводить касательную к кри­вой. На рис. 62б приводится прием построения касательной к кривой из точки, заданной вне кривой с помощью «кривой ошибок». Применение этого приема основано на том положении, что в искомой или заданной точке касания М длина хорды кривой равна нулю. Требуется провести через точку А каса­тельную t к кривой случайного вида. Для этого проведем через точку А пучок прямых, пересекающих кривую. Полу­ченные хорды делят пополам. Плавная кривая, проведенная через средние точ­ки («кривая ошибок»), в пересечении с заданной кривой определит искомую точку касания М.

Дата добавления: 2014-01-05