Тема 7. Рисунок 54 –Пересечение пирамиды фронтально проецирующей

А б

Б

А б

Рисунок 54 – Пересечение пирамиды фронтально проецирующей

плоскостью: а -модель, б – эпюр

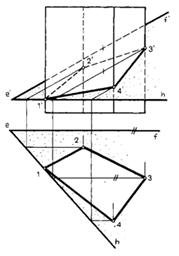Плоская фигура, которая получает­ся при пересечении многогранника пло­скостью, называется сечением. Постро­ение сечений значительно упрощается, если секущая плоскость является про­ецирующей. В этом случае одна проек­ция сечения совпадает с проецирующим следом плоскости.

1. Пересечение пирамиды фрон­тально проецирующей плоскостью. На рис. 49б фронтальная проекция а', b', с' сечения совпадает с фронталь­ным следом P_v секущей плоскости. Про­ведя линии связи до горизонтальных проекций соответствующих ребер мно­гогранника, получим горизонтальную проекцию сечения.

2. Пересечение прямой призмы пло­скостью общего положения (рис. 55). Секущая плоскость задана двумя пере­секающимися прямыми — горизон­талью и фронталью. Построение сече­ния, как и в предыдущей задаче, упро­щается, так как боковые грани призмы — горизонтально проецирующие плоско­сти. Следовательно, горизонтальная проекция сечения известна, она совпа­дает с горизонтальной проекцией боко­вых граней и ребер призмы.

Для построения фронтальной про­екции сечения необходимо спроециро­вать точки 1, 2, 3 и 4, принадлежащие секущей плоскости, на фронтальную проекцию. Воспользуемся какой-либо линией уровня, например фронталью (или любой другой прямой). Проводим через точки 2, 3 и 4 горизонтальные проекции фронталей, а затем строим фронтальные их проекции. В пересече­нии с соответствующими фронтальны­ми проекциями ребер получим искомые проекции точек пересечения ребер с плоскостью. Соединив полученные точ­ки прямыми в последовательности, ко­торая задана горизонтальной проек­цией, и определив невидимые участки сечения, закончим построение.

Итак, при построении пересечения многогранника плоскостью необходимо выделить частный случай, когда один из пересекающихся элементов (секущая плоскость или пересекаемая поверхность) занимает проецирующее по­ложение и одна проекция сечения из­вестна.

Рисунок 56 –Пересечение пирамиды плоскостью общего положения: а– модель, б – эпюр.  

а

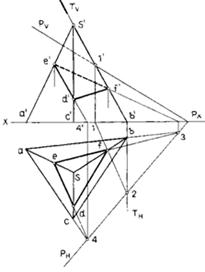
3. Пересечение пирамиды плоско­стью общего положения (рис. 56, а, б). В отличие от задачи, приведенной на рис. 54, здесь необходимо построить обе проекции сечения. Горизонтальный след секущей плоскости не пересекает основание пирамиды, следовательно, пересекается ее боковая поверхность. Сечение должно иметь форму треуголь­ника, вершинами которого будут точки пересечения ребер пирамиды с плоскостью. Точка пересечения ребра SB пи­рамиды с плоскостью Р найдена с по­мощью вспомогательной фронтально проецирующей плоскости Т. Аналогич­но могла быть построена точ­ка Е сечения. Однако можно применить и другой прием. Продолжим ребро АВ, которое является горизонтальным сле­дом грани ABS пирамиды, до пересече­ния с горизонтальным следом секущей плоскости в точке 3. Точки F и 3 при­надлежат линии пересечения EF дан­ной грани и секущей плоскости. По­строим третью точку D таким же спосо­бом, так как вспомогательная секущая плоскость, проведенная через ребро CS, будет параллельна профильной пло­скости проекции и не даст решения. Точка 4 является точкой пересечения горизонтальных следов грани ASC и се­кущей плоскости. Соединив получен­ные точки прямыми и выделив на фрон­тальной проекции невидимый участок e'f' сечения, закончим построение.

Подобную задачу можно решить и другим способом, преобразовав плоско­сть общего положения в проецирую­щую и приведя тем самым задачу к ви­ду, изображенному на рис. 54.

Рассмотрим типовые задачи на пересечение многогранников (призмы и пирамиды) плоскостями частного положения

Пример 1. Построить натуральную величину сечения пятиугольной призмы фронтально проецирующей плоскостью. Фигура сечения прямой пятиугольной призмы фронтально проеци­рующей плоскостью f^{/ /}_0α (рис. 57) представляет собой плоский пя­тиугольник 12345.

Для построения проекций фигуры сечения находят проекции точек пересечения плоскости f^{/ /}_0α с ребрами призмы и соединяют их прямыми линиями. Фронтальные проекции этих точек получаются при пересече­нии фронтальных проекций ребер призмы с фронтальным следом f^{/ /}_0α секущей плоскости а" (точки 1"—5").

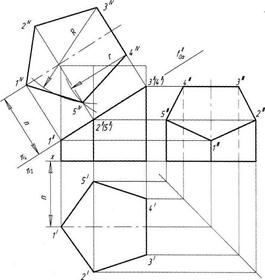
Рисунок 57 – Сечение призмы фронтально проецирующей плоскостью

Горизонтальные проекции точек пересечения 1^/—5' совпадают с го­ризонтальными проекциями ребер. Имея две проекции этих точек, с помощью линий связи находят профильные проекции 1"'—5'". Полу­ченные точки 1"'—5'" соединяют прямыми линиями и получают про­фильную проекцию фигуры сечения.

Действительный вид фигуры сечения определен способом замены плоскостей проекций. В данном примере горизонтальная плоскость проекций заменена но­вой π₄, причем ось π₂/π₄ (для упрощения построений) совпадает с фронтальным следом плоскости f^{/ /}_0α.

Пример 2. Построить натуральную величину сечения шестиугольной пирамиды фронтально проецирующей плоскостью.

Правильная шестиугольная пирамида, пересеченная фронталь­но проецирующей плоскостью f^{/ /}_0α, показана на рис. 58.

Фронтальная проекция сечения сов­падает с фронтальным следом f^{/ /}_0α плоскости. Горизонтальную и про­фильную проекции фигуры сечения строят по точкам, которые являются точками пересечения плоскости f^{/ /}_0α с ребрами пирамиды. Действитель­ный вид фигуры сечения в этом примере найдем способом перемены плоскостей проекций.

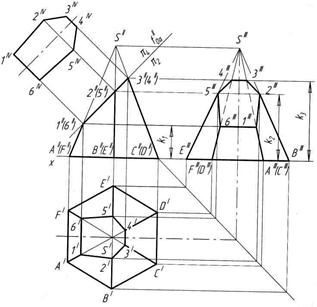
Рисунок 58 – Сечение пирамиды фронтально проецирующей плоскостью

Пересечение прямой линии с много­гранником. Задача определения точек пересечения прямой с поверхностью многогранника решается аналогично пересечению прямой с плоскостью. Ес­ли многогранник выпуклый, точек пе­ресечения две.

Эта задача решается в три этапа (рис. 59):

1) через данную пря­мую проводят вспомогательную секу­щую плоскость;

2) строят линию пере­сечения многогранника секущей пло­скостью;

3) определяют точки пересечения данной прямой с контуром сечения.

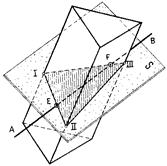
Рисунок 59 – Пересечение призмы прямой линией:

а - модель, б – эпюр

Полученные точки проецируют на другую плоскость проекций (e', f'), опре­деляют видимость точек пересечения и участков прямой (отрезок прямой е'—3' невидимый). Точки пересечения прямой с поверхностью многогранника называются точками встречи.

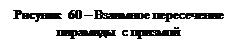Взаимное пересечение многогранников. Линия пересечения двух много­гранников представляет собой одну или две замкнутые ломаные линии. Отрезки ломаной линии являются линиями пе­ресечения граней, а точки излома — точками пересечения ребер одного мно­гогранника с гранями другого и ребер второго с гранями первого. Если один многогранник частично пересекается другим, то линия пересечения будет представлять собой одну замкнутую ло­маную линию, то такое пересечение назы­вают неполным. Если один многогран­ник полностью пересекается другим, то пересечение называют полным,при этом линия пересечения состоит из двух замкнутых ломаных линий.

Пересечение пирамиды с прямой призмой (рис. 60). Боковые ребра приз­мы проецируются в точки, а боковые ее грани являются горизонтально проеци­рующими отсеками плоскостей. Как это было ранее (см. рис. 54 и 55), следует выделить частный случай пересечения, когда одна проекция линии пересечения многогранников известна.

Точки пересечения ребер пирамиды с призмой легко определяются на гори­зонтальной проекции. С помощью ли­ний связи строим фронтальные проек­ции этих точек. Из вертикальных ребер призмы лишь одно ребро пересекает пи­рамиду. Точки пересечения этого ребра с гранями пирамиды определяем, про­водя вспомогательную горизонтально проецирующую плоскость S_H через ре­бро и вершину пирамиды. Она пересе­кает грани пирамиды по прямым, кото­рые пересекают ребро призмы в точках 7,7' и 8,8'. Соединяем построенные про­екции точек отрезками прямых в преде­лах каждой грани, при этом следует ру­ководствоваться горизонтальной про­екцией. Линия пересечения представ­ляет собой две замкнутые ломаные ли­нии. Пересечение полное. Видимыми являются те участки линии пересече­ния, которые принадлежат видимым граням многогранников.

Пересечение двух пирамид. Если пересекаются многогранники, у кото­рых пересекающиеся грани не являют­ся проецирующими, линию пересече­ния строят с помощью вспомогатель­ных проецирующих плоскостей, опре­деляя точки пересечения ребер одного многогранника с гранями другого, и на­оборот. Однако в некоторых случаях, когда пересекающиеся многогранники расположены своими основаниями на горизонтальной плоскости проекций, применение плоскостей общего поло­жения в качестве вспомогательных ока­зывается более рациональным и дает меньше дополнительных построений.

На рис. 61 приведен подобный при­мер. Через вершины пирамид проведе­на прямая и найден ее след М на пло­скости оснований пирамид. Вспомога­тельные плоскости, проведенные через прямую ST, пересекают грани по пря­мым линиям. Следы этих плоскостей проходят через точку m. Вспомогатель­ные плоскости образуют «пучок» плоско­стей, осью которого является прямая SM, соединяющая вершины многогран­ников.

Найдем точки пересечения ребра СТ с гранями пирамиды. Проведем вспомогательную плоскость Р через данное ребро и вершину S. Горизон­тальный след этой плоскости должен пройти через точку с — горизонталь­ный след ребра СТ. Вспомогательная плоскость пересечет стороны основа­ния другой пирамиды в точках 1 и 2, а ее грани — по прямым s1 s2, в пересе­чении с которыми и определяем гори­зонтальные проекции точек пересече­ния ребра СТ с пирамидой. Вторую вспомогательную плоскость Q прово­дим через ребро ВТ и строим точки пе­ресечения аналогичным образом. От­резки линии пересечения пирамид про­водим из точек пересечения вспомога­тельными плоскостями сторон основа­ний пирамид в пределах каждой пары пересекающихся граней. Третье ребро AT не пересекается с пирамидой EFDS. Полученные горизонтальные проекции точек и линий пересечения проецируем на фронтальную проекцию пирамид, выделяем невидимые участки линии пересечения.

Рисунок 61 – Взаимное пересечение двух пирамид

Дата добавления: 2014-01-05