Взаимное пересечение многогранников

ПРЯМОЙ ЛИНИЕЙ.

МНОГРАННЫЕ ПОВЕРХНОСТИ ОБЩИЕ СВЕДЕНИЯ. ПЕРЕСЕЧЕНИЕ МНОГРАННИКА ПЛОСКОСТЬЮ И

Все поверхности можно разделить на две большие группы: многогранные и кривые.

Многогранной назы­вается поверхность, образованная час­тями пересекающихся пло­скостей (рис. 52). Многогранником называется тело, ограниченное многогранной по­верхностью, состоящей из плоских мно­гоугольников. Части пересекающихся плоскостей назы­ваются гранями, а линии их пересече­ния — ребрами. Точки пересечения ре­бер называются вершинами. Совокуп­ность ребер и вершин многогранной по­верхности называется сеткой.

Многогранная поверхность называ­ется выпуклой, если она расположена по одну сторону от плоскости любой ее грани. Сечение выпуклого многогран­ника плоскостью — всегда выпуклый многоугольник.

Наиболее распространенные много­гранники — призмы и пирамиды. Приз­му, ребра которой перпендикулярны ос­нованию, называют прямой. Если в ос­новании прямой призмы — прямо­угольник, призму называют параллеле­пипедом.

Изображение на чертеже проекций многогранника есть, по существу, изображение проекций вершин (точек), ребер (прямых) и граней (плоскостей).

Видимость ребер многогранника. Необходимость в определении на эпюре видимости проекций ребер многогран­ника возникает постоянно. Иногда эта задача решается просто, однако в более сложных случаях целесообразно применить способ кон­курирующих точек, что дает безошибочное решение.

Рисунок 52 – Элементы многогранной поверхности

Внешний контур проекций много­гранника всегда видимый. Видимость ребер внутри контура следует опреде­лять на каждой проекции отдельно, рас­сматривая взаиморасположение ребер.

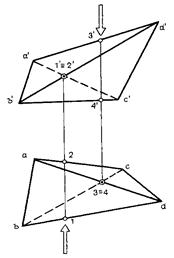На рис. 53 даны проекции четырех­гранника. На фронтальной проекции конкурирующими точками скрещиваю­щихся ребер являются точки 1 и 2, а на горизонтальной проекции — точки 3 и 4. Анализ взаиморасположения конку­рирующих точек позволяет установить, что на фронтальной проек­ции ребро BD будет видимым, а ребро АС — невидимым. На горизонтальной проекции ребро AD будет видимым, а ребро ВС — невидимым

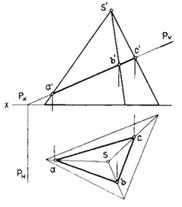
Пересечение многогранника пло­скостью. Линией пересечения поверх­ности многогранника плоскостью явля­ется плоский многоугольник. Его вер­шины являются точками пересечения ребер с заданной плоскостью, а стороны — линиями пересечения граней с плоско­стью (рис. 54а). Таким образом, по­строение сечения многогранника пло­скостью сводится к определению то­чек пересечения прямой с плоскостью или к определению линии пересечения плоскостей.

Дата добавления: 2014-01-05