Развертки. Построение разверток многогранных поверхностей и тел вращения

Развертывание поверхностей. В практике архитектурного проектирования и строительства раз­вертывание поверхностей находит при­менение при разработке чертежей для раскроя плоского листового материала. Способы развертки поверхностей используются при проектировании пнев­матических и тентовых сооружений, а также при строительстве резервуаров различной формы, воздуховодов и т. д.

Форма и размеры плоских фигур оп­ределяются специальными приемами развертывания по чертежам запроекти­рованных поверхностей. Построение разверток выполняется, как правило, только графическими приемами.

Развертыванием называется такое преобразование поверхности, в резуль­тате которого она совмещается с пло­скостью. Плоская фигура, полученная в результате развертывания поверхности и совмещения ее с плоскостью, называ­ется разверткой.

Ранее кривые поверхности бы­ли подразделены на развертываемые, которые могут быть совмещены с пло­скостью без разрывов и складок, и не-развертываемые. Развертывание по­следних выполняется приближенно при некоторой деформации или замене час­тей поверхности отсеками развертыва­емых поверхностей. Подобная замена отсеков одной поверхности отсеками другой, более простой поверхности на­зывается аппроксимацией.

Как отмечалось ранее, к разверты­ваемым относятся все гранные поверх­ности, а также кривые линейчатые по­верхности нулевой кривизны — цилин­дрические, конические и торсовые. На развертках этих поверхностей сохраня­ются длины отрезков линий, углы меж­ду пересекающимися линиями, величи­ны площадей замкнутых участков по­верхности. Такое преобразование про­странственной фигуры в плоскую назы­вают изометрическим отображением.

Следовательно, поверхность и ее развертку можно рассматривать как две ометрические фигуры, между точками которых установлено взаимно однозначное соответствие.

Изометрическое отображение по­верхности в плоскость включает два преобразования: одно из них, так назы­ваемое конформное, сохраняет инвари­антными (неизменными) величину уг­лов между линиями в точках их пересе­чения, а другое преобразование — эквиреальное, сохраняет величину пло­щадей замкнутой области поверхности.

Свойство сохранения величины площадей в таком преобразовании предопределяет и сохранение длины со­ответственных отрезков линий поверх­ности и ее развертки.

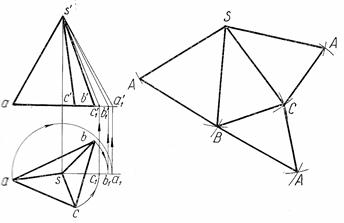
Рисунок 95 – Построение развертки пирамиды

Развертка многогранных поверхно­стей. Разверткой многогранной повер­хности называется плоская фигура, полученная в результате последова­тельного совмещения всех ее граней с плоскостью.

1. Развертка пирамиды (рис.95). Основание пирамиды парал­лельно плоскости Н, поэтому следует определить натуральную величину лишь бо­ковых граней — треугольников. Истин­ная длина боковых ребер пирамиды оп­ределена способом вращения вокруг вершины S. Затем по трем сторонам строят контуры боковых граней, которые соединяют друг с дру­гом смежными ребрами. К ним присое­диняется основание пирамиды. Если необхо­димо на развертке построить точку, принадлежащую боковой поверхности, то поступают следующим образом. Через точку и вершину пирамиды про­водят образующую, а затем – горизонталь, за­тем переносят на развертку натураль­ные величины проведенной образующей и горизонтали.

2. Развертка призмы. У прямой призмы все боковые ребра проецируют­ся в натуральную величину (рис. 96).

Развертку боковой поверхности призмы с рис. 57 с основанием и фигу­рой сечения призмы строят следующим образом (рис. 97). Проводят прямую, на которой откладывают пять отрезков, равных длинам сторон пятиуголь­ника, лежащего в основании призмы. Из полученных точек проводят перпендикуляры, на которых откладывают действительные длины ре­бер усеченной призмы, беря их с фронтальной или профильной проек­ции, получают развертку боковой поверхности призмы.

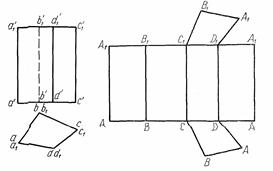
Рисунок 96 – Построение развертки призмы

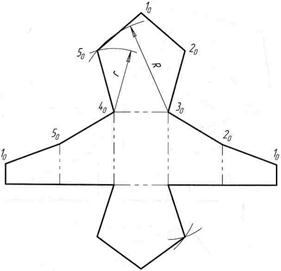
Рисунок 97 – Полная развертка усеченной призмы

К развертке боковой поверхности пристраивают фигуру нижнего основания — пятиугольник и фигуру сечения.

Развертка боковой поверхности усеченной пирамиды с рис. 58 с фигурой се­чения и фигурой основания приведена на рис. 98.

Сначала строят развертку неусеченной пирамиды, все грани кото­рой, имеющие форму треугольника, одинаковы. На плоскости намеча­ют точку S₀ (вершину пирамиды) и из нее, как из центра, проводят дугу окружности радиусом R, равным действительной длине бокового ребра пирамиды. Действительную длину ребра можно определить по про­фильной проекции пирамиды, например отрезки S"'E"' или S'"B'", так как эти ребра параллельны профильной плоскости и изображаются на ней действительной длиной. Далее по дуге окружности от любой точки, например, откладывают шесть одинаковых отрезков, равных дейст­вительной длине стороны шестиугольника — основания пирамиды. Действительную длину стороны основания пирамиды получают на го­ризонтальной проекции (отрезок А'В'). Точки А₀—Е₀ соединяют пря­мыми с вершиной S₀. Затем от вершины S₀ на этих прямых откладыва­ют действительные длины отрезков ребер до секущей плоскости.

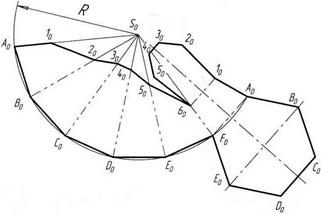
Рисунок 98 – Полная развертка усеченной пирамиды

На профильной проекции усеченной пирамиды имеются действи­тельные длины только двух отрезков — S'"5'" и S"2'". Действительные длины остальных отрезков определяют способом вращения их вокруг оси, перпендикулярной к горизонтальной плоскости и проходящей че­рез вершину S.

Полученные точки 1₀, 2₀, 3₀ и т. д. соединяют прямыми и пристраи­вают фигуры основания и сечения.

Развертка кривых поверхностей. Развертки поверхностей прямых круго­вых конусов и цилиндров могут быть выполнены точно. Полная развертка кругового цилиндра представляет собой боковую поверхность цилиндра – прямо­угольник со сторонами h и π D и два основания (верхнее и нижнее) диаметром D (рис. 99а).

Полная развертка кругового конуса состоит из боковой поверхности – сектора круга, радиус которого равен длине AS образующей конуса, а централь­ный угол при его вершине ψ =180°D/AS и основания конуса диаметром D (рис. 99б).

Полную приближенную развертку усеченного конуса с рис. 79 строят следующим образом (рис. 100). Построение сектора (см. рис. 100) выполняют с разбивкой его на равные части соответственно разметке образующих на чер­теже (см. рис. 79).

Дата добавления: 2014-01-05