Тема 9

Б

А

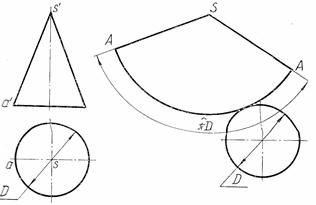
Рисунок 99 – Построение точных разверток: а – цилиндра, б – конуса

Используя положение образующих на чертеже и на разверт­ке, находят положение точек на развертке при помощи нату­ральных величин отрезков от вершины до соответствующих точек линии пересечения на чертеже. При этом расстояния S ₀ и S₀B₀ соответствуют фронтальным проекциям s'a' и s'b'. Отрез­ки образующих от вершины до других точек проецируются на фронтальную плоскость проекций с искажениями. Поэтому их натуральную величину находят вращением вокруг оси конуса до положения, параллельного фронтальной плоскости проек­ций.

На рис. 79 показано построение фронтальной и гори­зонтальной проекций точки К по изображению К₀ этой точки на развертке (см. рис. 100). Для построения проведена образу­ющая S₀13₀ через точку Ко на развертке. С помощью отрезка l₁ построена горизонтальная проекция 13. Через нее проведены горизонтальная s -13 и фронтальная s' - 13' проекции образу­ющей S—13. Отрезок So Ко = s'k'₁ отмечен на проекции образу­ющей s'7'. Обратным вращением построена фронтальная проекция k' точки К на фронтальной проекции образующей s'13'. Горизонтальная проекция к построена с помощью линии связи.

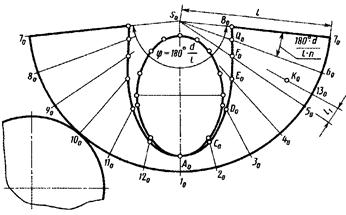
Рисунок 100 – Полная развертка усеченного конуса

Полную приближенную развертку усеченного цилиндра с рис. 80 строят следующим образом (рис. 101). Сначала строят полную развертку боковой поверхности цилиндра — пря­моугольник с высотой, равной высоте цилиндра, а длиной L, длину L переносят с горизонтальной проекции цилиндра замеряя хорды, например, 7 – 8 и так последовательно пока не перенесут все хорды на прямую. Для построения на раз­вертке точек линии среза развертку основания цилиндра де­лят на такое же число частей, как и при построении проекций линий среза. Проводят через точки деления образующие и, пользуясь фронтальной проекцией, отмечают на них высоту до точек эллипса среза, например, точка 1₀ . Соединяют построенные точки плав­ной кривой. Натуральный вид фигуры среза цилиндра плоскостью, выполненный ранее на рис. 80, переносят и пристраивают к развертке.

Построим на чертеже цилиндра проекции точки М, указан­ной на развертке точкой М₀. Для этого отметим хорду l₂ между образующей, на которой расположена точка М₀, и образую­щей точки 4. По хорде l₂ строим горизонтальную проекцию т (рис. 80) и по известной высоте ее расположения находим ее фронтальную проекцию т'.

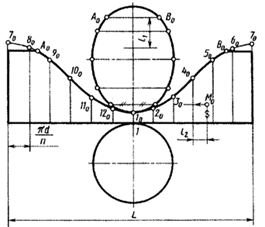
Рисунок 101 – Полная развертка усеченного цилиндра

Построение развертки поверхности наклонной призмы или наклонного цилиндра. Чтобы построить развертку боковой поверх­ности наклонной призмы, можно применить один из следующих способов:

а) способ треугольников (или триангуляции);

б) способ построения нормального сечения;

в) способ раскатки.

Сущность способа треугольников состоит в том, что каждая грань призмы диагональю разбивается на два треугольника, затем опре­деляются истинные величины всех сторон треу­гольников, которые последовательно в истин­ную величину вычерчиваются на свободном поле чертежа.

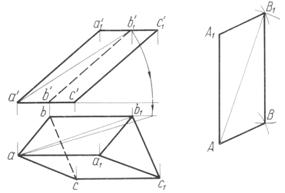
На рис. 102 этот способ применен для постро­ения развертки боковой поверхности трехгран­ной наклонной призмы.

Грань AВВ₁A₁ диагональю AВ₁ разделена на два треугольника.

Для построения истинной величины треуголь­ника A A₁В₁ надо определить истинную величи­ну только одной его стороны — стороны AВ₁, так как в приведенном примере две другие сто­роны этого треугольника расположены относи­тельно плоскостей проекций так, что одна из их проекций является истинной величиной: истин­ная величина стороны A₁В₁ — ее горизонталь­ная проекция а₁b₁, стороны AВ₁ —фронтальная а^/а₁^/.

Истинная величина стороны AВ₁ на рис. 102 определена вращением ее вокруг оси, перпен­дикулярной к плоскости проекций V и прохо­дящей через точку А. Затем к построенному в натуральную величину по трем сторонам тре­угольнику A A₁В₁ пристроен треугольник AВВ₁, истинные величины всех сторон которого уже известны. Далее следует диагональю разделить на два треугольника вторую грань призмы, оп­ределить истинные величины всех сторон этих треугольников и построить их в натуральную величину примыкаемыми к первым двум, затем разделить на два треугольника следующую грань призмы и т. д.

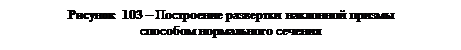
На рис. 103 развертка боковой поверхности трехгранной наклонной призмы построена спо­собом нормального сечения. Последователь­ность построений следующая:

1) призма рассекается нормальной (перпен­дикулярной к ее ребрам или граням) пло­скостью. В приведенном примере нормальной плоскостью является фронтально проецирую­щая плоскость Р, горизонтальный след которой на эпюре не показан;

2) строятся проекции и определяется истин­ная величина фигуры нормального сечения. На рис. 103 фронтальная проекция фигуры нормального сечения (1^/ — 2'—3') совпадает со следом секущей плоскости, а горизонталь­ная не показана. Истинная величина фигуры сечения (1₀ —2₀ — 3₀) построена способом сов­мещения — плоскость Р вращением вокруг ее горизонтального следа совмещена с плоско­стью проекций Н;

3) истинная величина фигуры нормального сечения на свободном поле чертежа разворачи­вается в прямую линию (1— 1) и от точек 1,2, 3, 1 проводятся перпендикуляры к прямой 1- 1;

4) на перпендикулярах по обе стороны от
точек 1, 2, 3, 1 откладываются истинные вели-
чины соответствующих ребер призмы и полученные точки А, В, С, А и А_1, В₁,C₁, А₁ соединяются отрезками прямых. В рассматриваемом примере ребра призмы параллельны плоскости проекций V, аследовательно, истинными величинами их являются соответствующие
фронтальные проекции.

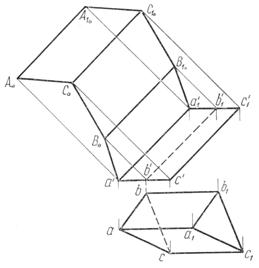
Способ раскатки применим тогда, когда реб­ра призмы параллельны одной из плоскостей проекций, например плоскости проекций V на рис. 104. При этих условиях каждую грань призмы последовательно поворачивают вокруг одного из ребер, как вокруг фронтали, до по­ложения, параллельного плоскости проекций V; все грани призмы спроецируются на пло­скость проекций V в натуральную величину. Практически построения выполняются так. Из фронтальных проекций точек А, В, С, А₁, В₁, C₁ проводятся перпендикуляры к ребрам призмы (рис. 104).

В рассматриваемом примере раскатка боко­вой поверхности призмы начата с грани А ВВ₁ А₁. Чтобы повернуть ее вокруг ребра А А₁ до положения, параллельного плоскости про­екций V, из точек а^/ и а₁^/ на перпендикулярах, выходящих из точек b ^/ и b₁^/, сделаны засечки раствором циркуля, равным истинной величи­не стороны АВ (А₁ В₁) основания призмы (истинной величиной стороны АВ основания призмы является ее горизонтальная проекция ab). Параллелограмм а^/В₀ В_1о а₁^/ есть истинная величина грани А ВВ₁ А₁. Затем из точек В₀ и В_1о раствором циркуля, равным истинной ве­личине стороны ВС (В₁С₁) основания призмы, сделаны засечки на перпендикулярах, выхо­дящих из точек с' и с — параллелограмм ВоСоС_1оВ_1о — истинная величина грани ВВ₁С₁С призмы. Истинная величина грани CC₁A₁A по­строена аналогично. Фигура a'B_oC_oA_oA_1oС_1oВ_1о а₁^/ — развертка боковой поверхности призмы.

Если необходимо построить развертку пол­ной поверхности призмы, к построенной раз­вертке боковой поверхности ее надо пристро­ить истинные величины оснований.

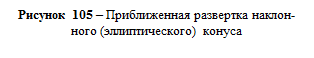Для построения развертки поверхности на­клонного цилиндра следует вписать в этот ци­линдр многогранную призму, построить раз­вертку поверхности ее, а затем полученные точки соединить не ломаной, а плавной кривой линией.

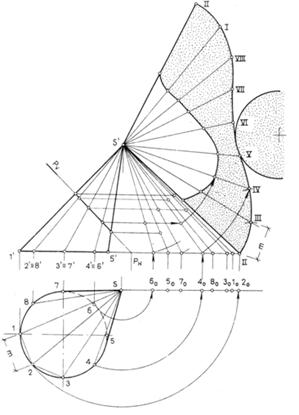
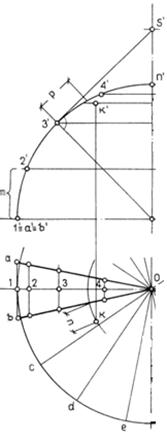
Приближенная развертка наклон­ного (эллиптического) конуса (рис.105). Боковая поверхность конуса аппрок­симируется вписанной в нее многогран­ной поверхностью пирамиды, которая и развертывается. Натуральные величи­ны боковых ребер (образующих конуса) определены вращением. Преобразо­ванной точкой вершины конуса приня­та ее фронтальная проекция. Контур развертки боковой поверхности постро­ен по точкам засечками из точки s' ра­диусом, равным длине образующей, и отрезком m, равным стороне много­угольника основания вписанной пира­миды.

Граничные точки ребер пирамиды соединены плавной кривой. Поверх­ность конуса разрезана по образующей S2. Развертка боковой поверхности ог­раничена двумя прямыми — образую­щими и кривой линией — преобразо­ванной граничной контурной линией конуса. На развертке показана линия пересечения конуса фронтально про­ецирующей плоскостью. Эллиптиче­ская кривая сечения поверхности кону­са преобразуется в другую плоскую кривую развертки боковой поверхно­сти.

		б
	а
		а

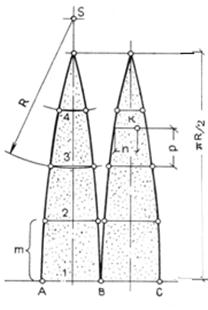
Развертка сферы. Сферическая поверхность неразвертываема. Ее нельзя развернуть на плоскость без раз­рывов и складок. Для неразвертываемых поверхностей строят условные раз­вертки. Один из способов развертки за­ключается в аппроксимации (замене) сферических элементов сферы цилинд­рическими (рис. 106а). Для этого по­верхность сферы делится меридианами на части. Участки поверхности, заклю­ченные между смежными меридианами, заменяются цилиндрической поверхно­стью, которая и развертывается.

В нашем примере поверхность полу­сферы разделена меридианами на 16 равных частей, которые проецируются на горизонтальную плоскость Н секто­рами. Часть сферической поверхности, заключенную между смежными мери­дианами АО и ВО, заменим цилиндри­ческой поверхностью, касательной к сфере по главному меридиану. Разде­лим фронтальную проекцию этого эле­мента на четыре равные части. Опреде­лим горизонтальные проекции отрезков образующих 1, 2, 3 и 4 цилиндрического элемента.

Построим развертку этого элемента цилиндрической поверхности. На сво­бодном месте чертежа (рис. 106б) наме­тим ось симметрии элемента и отложим на ней четыре раза отрезок т — рас­стояние между делениями главного ме­ридиана. В полученных точках откладываем по горизонтали отрезки образу­ющих цилиндрического элемента, взя­тые с плана.

Если развертываемый элемент по­верхности начинается с экватора сфе­ры, этот его отрезок (отрезок 1) изобра­жается прямым. Если же элементы раз­вертки начинаются с какой-либо про­межуточной параллели сферы (напри­мер, когда поверхность представляет собой сферический сегмент), то на раз­вертке эта параллель изобразится ду­гой окружности (отрезок 3). Радиус этой окружности определяется на фронталь­ной проекции с помощью касательной s'3^/ проведенной к очерку сферы в со­ответствующей точке, до пересечения с осью. Положение точки К, принадлежа­щей сфере, определяют на развертке с помощью двух измерений р и п ("коор­динаты" точки), взятых на фасаде и плане.

Дата добавления: 2014-01-05