Аксонометрические проекции

На практике весьма часто возникает необходимость в на­глядном изображении предмета на чертеже, т. е. в изображении его в трех измерениях. Это до­стигается аксонометрическими проекциями, сущность которых заключается в том, что изобра­жаемый предмет располагает­ся по отношению к некоторой плоскости проекций так, что при параллельном проецирова­нии на нее ни одна из осей ко­ординат, к которым он отнесен в пространстве, не проецирует­ся на плоскость проекций в ви­де точки. В результате ни одно из измерений изображаемого предмета не исчезает, и он про­ецируется на плоскость проекции в трех измерениях, а не в двух, как это получается при прямоугольном параллельном проецировании на три взаимно перпендикуляр­ные плоскости проекций (рис. 107).

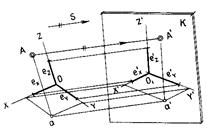
Рисунок 107 – Образование аксонометрических проекций

Аксонометрическими проекци­ями называют наглядные изображе­ния объекта, получаемые параллель­ным проецированием его на одну пло­скость проекций вместе с осями пря­моугольных координат, к которым этот объект отнесен.

Основная теорема аксонометрии. При изменении взаимного положения осей координат и направления проеци­рования относительно плоскости про­екций изменяются положение аксоно­метрических осей и показатели искаже­ния по ним. Этому вопросу посвящена основная теорема аксонометрии (теоре­ма Польке–Шварца): три произвольно выбран­ных отрезка на плоскости, выходящие из одной точки, могут быть приняты за параллельную проекцию трех рав­ных и взаимно перпендикулярных от­резков, выходящих из некоторой точ­ки пространства.

Таким образом, из теоре­мы следует, что аксоно­метрические оси и показатели искаже­ния по ним могут быть выбраны произ­вольно. Если задать на плоскости про­екций К (см. рис.107) три проходящие через одну точку отрезка произвольной длины е'_х, е'_у и е'_z, можно утверждать, что они являются аксонометрической про­екцией трех равных и взаимно перпен­дикулярных отрезков пространства.

Размеры изображаемого предмета при аксонометрическом проецирова­нии по всем трем осям искажаются, это следует из теоремы.

В зависимости от расположения плоскости проекций и направления проецирования воз­можны случаи, когда показатели искажения по всем трем осям одинаковы, или равны между собой только по двум осям, или показатели ис­кажения по всем трем осям не равны между собой. Соответственно этому аксонометричес­кие проекции называют изометрическими (износ — одинаковый), диметрическими (ди— двойной) и триметрическими.

Аксонометрические проекции бывают также прямоугольные (когда направление проециро­вания составляет с плоскостью проекций пря­мой угол) и косоугольные.

На практике применяются только некоторые определенные направления аксонометрических осей и определенные величины показателей искажения (табл. 2).

Выбор аксонометрических проек­ций. Выбор аксонометрических проек­ций при построении изображений может подчиняться различным требованиям. Главные из них — наглядность и простота построений.

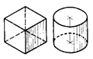
Сравнительная оценка изображе­ний, построенных в различных аксоно­метрических проекциях (табл. 2), по­казывает, что самым наглядным изо­бражением, лишенным заметных иска­жений формы, является прямоугольная диметрия. В прямоугольной изометрии одинаковый ракурс боковых граней куба делает изображение многогранника недо­статочно наглядным, а вот наглядность тел вращения не теряется, поэтому диметрия рекомендуется для всех геометрических тел, а вот в изометрии рекомендуют изображать лишь тела вращения. В прямоугольной диметрии этот недостаток отсутствует.

Выбирая тот или иной вид косо­угольной аксонометрической проекции, следует иметь в виду, что наряду с не­изменностью формы одной части объек­та возникают заметные искажения дру­гих его частей. Изображенные объекты воспринимаются несколько деформи­рованными, со скошенностью в направ­лении, перпендикулярном плоскости проекции.

В машиностроении принято использовать прямоугольное проецирование. Для прямоугольного проецирования: к² + т² + п²=2.

Кроме этого, сумма квадратов двух любых показателей искажения не может быть меньше единицы.

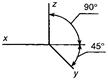
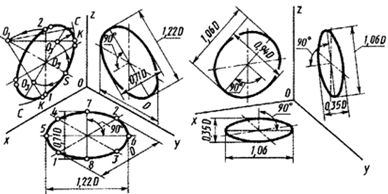
Прямоугольная изометрическая проекция. При равном наклоне аксонометрической пло­скости проекций ко всем трем осям координат и прямоугольном проецировании эта система спроецируется на плоскость проекций так, как показано на рис. 108а. Показатели искажения в этом случае по всем трем осям оказываются одинаковыми и равными 0, 82. Это прямоуголь­ная изометрическая проекция. Но для упроще­ния построений на практике применяют так на­зываемые приведенные показатели искажения, равные единице, т. е. размеры изображаемого предмета по всем трем осям откладываются в натуральную величину, а изображение пред­мета в связи с этим оказывается увеличенным в 1,22 раза по отношению к его истинной вели­чине.

На рис. 108а изображена окружность в прямоугольной изо­метрической проекции d. Из рисунка видно, что все три окружности, каждая из ко­торых расположена параллельно одной из пло­скостей проекций, проецируются на них в виде равновеликих эллипсов, большие оси которых равны 1,22d и расположены перпендикулярно к осям, отсутствующим в данных плоскостях, а малые равны 0,7d.

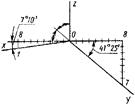
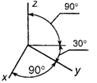
Прямоугольная диметрическая проекция. При некотором расположении аксонометри­ческой плоскости проекций относительно про­странственной координатной системы и прямо­угольном проецировании координатная систе­ма спроецируется на плоскость проекций, как показано на рис. 108б. Это прямоугольная ди­метрическая проекция.

Таблица 2 – Аксонометрические проекции

Вид проекций	Расположение осей	Изображение геометрических тел	Коэффициенты искажения
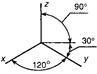
Прямоугольная изометрия			kx=ky=kz= = 0,82≈ 1,0
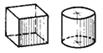
Прямоугольная диметрия			kx=kz= = 0,94≈ 1,0 ky= 0,47 = ≈ 0,5
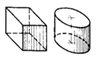
Косоугольная фронтальная изометрия			kx=ky=kz= = 1,0
Косоугольная горизонтальная изометрия			kx=ky=kz= = 1,0
Косоугольная фронтальная диметрия			kx=kz= 1,0 ky= 0,5

Действительные показатели искажения в прямоугольной диметрической проекции по осям X и Z равны 0,94, а по оси У — 0,47, при­веденные—соответственно 1,0 и 0,5, в резуль­тате чего изображение на чертеже оказывается увеличенным по отношению к истинной вели­чине в 1,06 раза.

Изображение окружности в диметрии приведено на рис. 108б. Окруж­ность, находящаяся в плоскости проекций XOZ (или в параллельной ей плоскости), проециру­ется на нее в виде эллипса, большая ось кото­рого равна l,06d, а малая — 0,94d. Окружно­сти, находящиеся в плоскостях, параллельных двум другим плоскостям проекций, проециру­ются на них в виде одинаковых эллипсов, боль­шие оси которых равны l,06d, а малые — 0,35d. Большие оси эллипсов, так же как и в прямоу­гольной изометрии, перпендикулярны к отсут­ствующим в данной плоскости аксонометричес­ким осям.

Дата добавления: 2014-01-05