Библиографический список. Рисунок 108 –изображение окружности в: а –изометрии; б –диметрии

А б

А б

А б

Рисунок 108 – Изображение окружности в: а – изометрии; б – диметрии

Для иллюстрации выполним построение усеченных призмы, пирамиды, цилиндра и конуса в аксонометрической про­екции.

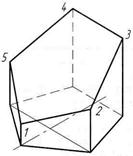
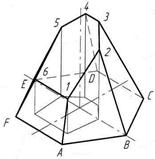
Рисунок 109 -Изометрическая проекция: а – усеченной призмы, б – усеченной пирамиды

На рис. 109а построена изомет­рическая проекция усеченной призмы с рис. 57. По­рядок построения изометрической проек­ции следующий. Строят изометрическую проекцию основания призмы; проводят в вертикальном направлении линии ребер, на которых от основания откладывают их дей­ствительные длины, взятые с фронтальной или профильной проекции призмы. Полу­ченные точки 1—5 соединяют прямыми ли­ниями.

Построение изометрической проекции усеченной пирамиды с рис. 58 (рис. 109б) начи­нают с построения изометрической проекции основания пирамиды по размерам, взятым с горизонтальной проекции комплексного чертежа. Затем на плоскости основания по координатам точек 1^/—6' строят го­ризонтальную проекцию сечения (тонкие линии на основании пирамиды). Из вершины полученного шестиугольника проводят вертикальные прямые, на которых откладывают координаты, взятые с фронтальной или профильной проекции призмы. Полученные точки 1—6 соединяют, получают фигуру сечения. Соединив точки 1—6 с вершинами шестиугольника, основа­ния пирамиды, получают изометрическую проекцию усеченной пирами­ды. Невидимые ребра изображают штриховыми линиями.

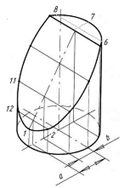
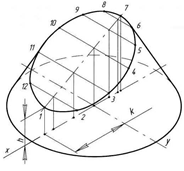
Рисунок 110 – Изометрическая проекция усеченного:

а – цилиндра, б – конуса

Изометрическую проекцию усеченного цилиндра строят следую­щим образом (рис. 110а).

Сначала строят изометрию нижнего основания (эллипс) по восьми точкам, рассчитав предварительно значения большой и малой осей эллипса. Затем пристраивают полную боковую поверхность, отложив высоту цилиндра и верхнее основание цилиндра. По трем координатам (рис. 80), отложенным по соответствующим осям, и соединенным линиями параллельными соответствующим осям строят точки сечения цилиндра плоскостью в аксонометрии. Полученные точки соединяют по лекалу. Заканчивают построение проведением очерковых образующих, касательных к основаниям эл­липса.

Построение изометрической проекции усеченного конуса (рис. 110б) начинают с построения основания — эллипса. Изометрическую проекцию любой точки кривой сечения находят при помощи трех координат, как показано на рис. 79.

На оси х откладывают координаты точек 1—7, взятые с горизон­тальной проекции конуса (рис. 79). Из полученных точек проводят вертикальные прямые, на ко­торых откладывают координаты z, взятые с фронтальной проекции точек, обозначенных буквами латинского алфавита. Через полученные на наклонной оси эллипса точки проводят прямые, параллельные оси у, и на них откладывают отрезки 6'8', 4' 10' и т. д., взятые на горизонталь­ной проекции. Найденные точки соединяют. Крайние очерковые обра­зующие проводят по касательной к контуру основания конуса и эллипса.

На практике рекомендуется аксонометрические проекции многогранников чертить в прямоугольной диметрии, а тела вращения – в прямоугольной изометрии.

ВОПРОСЫ К ЭКЗАМЕНУ:

1. Предмет и метод начертательной геометрии.

2. Точка и прямая.

3. Взаимные положения прямых.

4. Виды проецирования.

5. Ортогональное проецирование.

6. Эпюр Монжа.

7. Чертежи точек.

8. Чертежи отрезков прямых линий.

9. Взаимное положение двух прямых.

10. Следы прямой.

11. Плоскость. Задание плоскости на чертеже.

12. Расположение плоскости относительно плоскостей проекций.

13. Прямая и точка в плоскости.

14. Пересечение плоскостей и прямой плоскостью.

15. Перпендикулярность и параллельность прямой и плоскости.

16. Перпендикулярность и параллельность двух плоскостей.

17. Главные линии плоскости.

18. Способы преобразования проекций.

19. Способ замены плоскостей проекций.

20. Способ вращения.

21. Вращение вокруг проецирующей оси.

22. Плоскопараллельное перемещение.

23. Поверхности. Классификация, способы задания, определитель поверхности.

24. Линейчатые поверхности.

25. Кривые линии и поверхности.

26. Поверхности вращения с образующей прямой линией.

27. Поверхности вращения с образующей кривой линией.

28. Точка на поверхности.

29. Главные позиционные задачи.

30. Главные метрические задачи.

31. Пересечение поверхностей прямой линией.

32. Сечение поверхностей плоскостью.

33. Взаимное пересечение поверхностей. Способы построения линий пересечения поверхностей.

34. Пересечение многогранников плоскостью и прямой линией.

35. Взаимное пересечение многогранников.

36. Взаимное пересечение криволинейной поверхности с многогранной.

37. Взаимное пересечение кривых поверхностей.

38. Метод сфер.

39. Особые случаи пересечения поверхностей.

40. Развертки поверхностей.

41. Развертки многогранников.

42. Построение развертки поверхности наклонной призмы или цилиндра.

43. Точные и приближенные развертки.

44. Условные развертки неразвертывающихся поверхностей.

45. Развертка сферы.

46. Аксонометрические проекции.

47. Основная теорема аксонометрии.

48. Прямоугольные изометрические проекции.

49. Прямоугольные диметрические проекции.

50. Окружность в прямоугольной изометрической и диметрических проекциях.

2. Государственные стандарты единой системы конструкторской документации.

3. Ю.И. Короев Начертательная геометрия: учеб. / Ю.И. Короев. - 3-е изд., стер. – М.: КНОРУС, 2011. – 432 с.

4. В.П. Куликов, А.В. Кузин, В.М. Демин. Инженерная графика / В.П. Куликов, А.В. Кузин, В.М. Демин, – 2-е изд., испр. и доп. – М.: ФОРУМ: ИНФРА-М, 2007. – 368 с.

5. П.Г. Талалай. Начертательная геометрия на примерах. – СПб.: БЧВ-Петербург, 2011. – 288 с.: ил.

6. А.А. Чекмарев. Начертательная геометрия и черчение: учеб. для вузов / А.А. Чекмарев. – 3-е изд., перераб. и доп. –М.: Юрайт; ИД Юрайт, 2011. – 471 с.

Содержание

Стр.

Предисловие…………………………….…………………………………..
Обозначения и символы………………………………….………………..
Введение…………………………………………..……………………........ Тема 1.Предмет и метод начертательной геометрии. Метод проекций. Виды проецирования. Свойства ортогонального проецирования. Пространственная модель координатных плоскостей проекций. Эпюр Монжа…………………………………………....................... Тема 2. Чертежи точек. Чертежи отрезков прямых линий. Определение длины отрезка прямой. Следы прямой линии……………………… Тема 3. Взаимные положения прямых. Проекции плоского угла….. Тема 4. Плоскость. Прямые и точки в плоскости. Взаимное положение двух плоскостей. Позиционные задачи. Метрические свойства прямоугольных проекций…………………………………………………... Тема 5. Способы преобразования проекций. Способ замены плоскостей проекций. Способ вращения. Способ плоскопараллельного перемещения. Способ совмещения…………………………………………...
Тема 6. Многранные поверхности. Общие сведения. Пересечение многранника плоскостью и прямой линией. Взаимное пересечение многогранников…………………………………………………………….. Тема 7. Кривые линии. Основные понятия и определения. Кривые поверхности. Построение касательной к кривой поверхности. Пересечение кривых поверхностей плоскостью и прямой линией. Взаимное пересечение поверхностей. Метод сфер…………………………………... Тема 8. Развертки. Построение разверток многогранных поверхностей и тел вращения………………………………………………………… Тема 9. Аксонометрические проекции………………………..…..........
Вопросы к экзамену…………………………………………………..........
Библиографический список………………………………………………

Авторы - Т.В. Семенова, Е.В. Петрова

Дата добавления: 2014-01-05