Перехідні процеси при короткому замиканні у колі з R та L

Розглянемо коло з послідовним з’єднанням R та L (рис. 13.5).

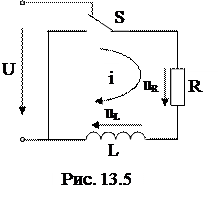Нехай при t=0 активний опір R та індуктивна котушка L замикаються накоротко за допомогою вимикача S.

Знайдемо закон зміни струму у колі після замкнення вимикача S.

Задаємося додатнім напрямом перехідного струму i та напрямом обходу контуру. Визначимо незалежні початкові умови, для чого розрахуємо коло до комутації:

.

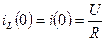Перехідний процес у колі описується рівнянням:

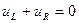або .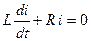

Дане диференційне рівняння є однорідним. Тобто сталий струм буде дорівнювати нулю, а перехідний процес зумовлений тільки енергією, яка запасена у магнітному полі котушки. Тому рішення диференційного рівняння буде таким:

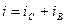, (13.1)

де: 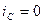, тому і= і_в .

Визначимо 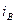. Для цього вирішимо однорідне диференційне рівняння:

.

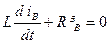Рішення цього рівняння має вигляд: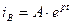

де 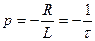– корінь характеристичного рівняння ;

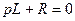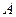– стала інтегрування, яка визначається з початкових умов:

при t=0: ,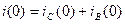

де і_в(0)=А е⁰=А, тому завжди А= і(0)-і_с (0),

тоді рішення (13.1) можна записати так:

і=і_с+ [і(0)-і_с (0)]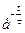. (13.2)

Це є загальна форма рішення диференційного рівняння, що описує перехідний процес в лінійному колі з одним накопичувачем енергії.

В нашому випадку .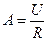

Отже ,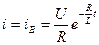

тобто струм зменшується по експоненті.

Затухання вільної складової ПП характеризується сталою часу кола:

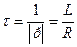[с]

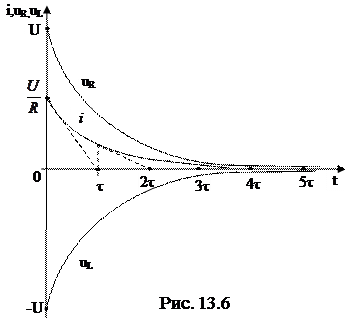Сталою часу кола називається величина інтервалу часу, за який вільні складові струму чи напруги зменшуються в е (е = 2,71…) раз.

Сталу часу можна визначити графічно, як довжину довільної піддотичної до експоненти (рис. 13.6). При використанні формули (13.2) τ знаходять відносно полюсів С чи L.

Теоретично ПП у колі триває нескінченно довго, а практично .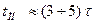

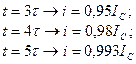
Величина, обернена до сталої часу, зветься коефіцієнтом згасання .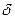

Для кола R, L:

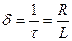[1/с].

Отже, вільний струм у колі затухає тим швидше, чим більше R та чим менше L.

Напруга 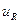у контурі R, L буде дорівнювати:

.

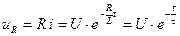Напруга на активному опорі змінюється аналогічно струму.

Напруга на індуктивній котушці :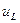

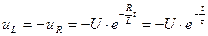
Напруга 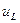в момент комутації змінюється стрибком від 0 до 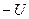, це видно на графіку рис. 13.6.

ПП у контурі R, L зумовлений енергією, яка запасена в магнітному полі котушк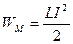и . При 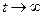ця енергія перетворюється в теплову: .

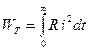Підставивши значення перехідного струму, отримаємо:

.

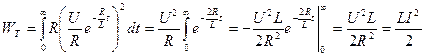Отже, кількість тепла, яка виділяється на резисторі 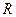, дорівнює енергії, яка запасена у магнітному полі котушки.

Якщо в схемі рис 13.5 просто розімкнути коло, то струм в котушці практично миттєво зменшиться до нуля 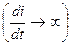. При цьому у котушці буде наводитися дуже велика ЕРС самоіндукції 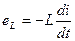. Виникаюче при цьому перенапруження у котушці може призвести до пробою ізоляції, пошкодженню та виходу з ладу рубильника тощо. Тому при вимкненні котушок від мережі їх замикають накоротко або на розрядний резистор.

Дата добавления: 2014-01-05