Аксиомы Неймана-Моргенштерна

Аксиома транзитивности. Предпочтения ЛПР являются транзитивными. Например, если субъект предпочитает исход А исходу В, а исход В исходу С, то следовательно, он предпочитает исход А исходу С.

Аксиома безразличия. Если имеется три возможных исхода А, В и С, а ЛПР предпочитает исход А исходу В, а исход В – исходу С, то должна существовать такая вероятность Р, что для ЛПР следующие две альтернативы будут иметь одинаковую ценность:

· получить В наверняка;

· игра, в которой ЛПР выигрывает А с вероятностью Р, либо выигрывает С с вероятностью (1–Р). Значения вероятности могут быть различными, что не имеет принципиального значения. Важно то, что существует определенное значение вероятности Р, при котором для ЛПР будет безразлично: либо принять участие в игре, в которой можно выиграть А или С, либо получить выигрыш В.

Аксиома рациональности. Если ЛПР предложено два лотерейных билета с идентичными призами, то он выберет билет с большей вероятностью выигрыша.

Однако следует заметить, что не все экономисты и статистики разделяют эти аксиомы, но большинство все-таки рассматривает их как вполне разумные допущения, позволяющие строить теорию выбора решения в условиях неопределенности. Также, необходимо отметить, что не все индивидуумы действуют согласно этим аксиомам. Даже если человек согласен со всеми из них, это отнюдь не предполагает, что он не может ошибиться и совершить нерациональное действие. Смысл этих аксиом заключается в том, что они показывают, как люди должны принимать решения для того, чтобы эти решения согласовывались с их предпочтениями, хотя на практике менеджеры не всегда принимают решения, согласующиеся с ними.

Теорема. Каждому результату лотереи можно приписать некоторое число такое, что для любых двух лотере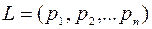й и 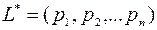будет верно 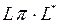тогда и только тогда, когда .

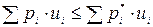Число 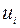, приписываемое i-му результату, называется его полезностью.

Число 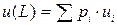, которое приписывается лотерее L, называется средней ожидаемой полезностью лотереи. Это математическое ожидание этой лотереи.

Принцип фон Неймана-Моргенштерна:

Индивидуум будет поступать так, чтобы максимизировать значение полезности.

Функция полезности возрастает, причем она линейна, если ЛПР нейтрален к риску, вогнута, если ЛПР несклонен к риску, и выпукла, если ЛПР склонен к риску.

Функция несклонности к риску:

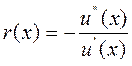
Дата добавления: 2014-01-05