Третья функция сложного процента

Эта функция, являясь обратной ко второй, определяет размер вносимой вначале каждого промежутка времени суммы 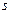с целью получения в конце периода итоговой суммы размера при определенном проценте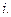

Исходной здесь является вторая функция сложного процента (1.6). Из нее можно найти

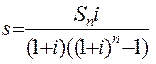(1.10)

Сумма 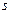называется авансовой суммой фонда возмещения, а величина

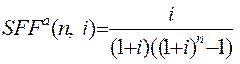(1.11)

авансовым фактором фонда возмещения.

Пример 1.2. Необходимо в течение 10 лет накопить сумму в размере 150000 у.е. для приобретения земельного участка с гостиницей. Какую сумму необходимо депонировать в начале каждого года при годовом проценте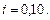

Решение: На основании (1.10)

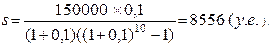
Если в качестве исходной функции брать (1.8), то на ее основе третья функция будет определена так

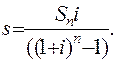(1.12)

Ее называют обычной суммой фонда возмещения, а величину

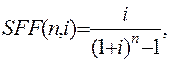(1.13)

обычным фактором фонда возмещения.

Дата добавления: 2014-01-05