Текущая стоимость актива

Будем считать, что актив в конце года приносит чистый операционный доход I.

В дальнейшем будем писать просто доход.

К концу срока экономической жизни 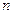он должен создать стоимость

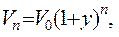(2.1)

где 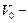начальная стоимость актива,

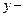норма отдачи на капитал,

создаваемая активом стоимость в течение его экономической жизни.

Согласно шестой функции сложного процента ежегодный доход 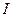с данного актива определится из равенства

(2.2)

на основе которого можно найти

(2.3)

Отметим, что (2.3) является аналогом (1.21), при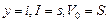

Выражение (2.3) записывается еще так [2]

Величину I можно представить в виде двух составляющих

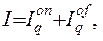(2.4)

где часть дохода представляющая собой доход на капитал,

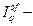часть дохода, поступающая в фонд возмещения актива,

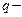номер года эффективной жизни актива.

Фонд возмещения – это фонд восстановления первоначальной стоимости актива 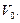К концу экономической жизни актива накопления в фонде возмещения должны cоставить величину Это значит, что должно выполняться равенство

из которого следует

(2.5)

Ежегодный доход на капитал равен

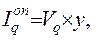(2.6)

где текущая стоимость актива.

Для определения стоимости актива 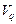на конец года q рассмотрим составляющие 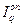и 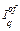по годам эксплуатации актива.

Для упрощения изложения введем обозначение

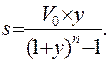(2.7)

Тогда в конце первого года будет

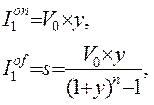(2.8)

а стоимость актива составит величину

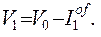(2.9)

В конце второго года

(2.10)

(2.11)

В (2.10) первый член доход, создаваемый предыдущим взносом (в данном случае взносом первого года) в фонд возмещение. А второй член 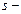новый взнос в фонд возмещения в конце второго года.

Аналогично для третьего года

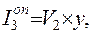(2.12)

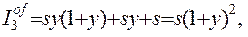(2.13)

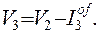(2.14)

Для года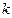

(2.15)

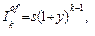(2.16)

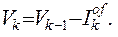(2.17)

Графически накопление величины представлено на рисунке 2.1.

Значение является стоимостью актива в конце года эксплуатации Найдем его окончательное выражение на любой момент.

Следуя (2.9) с учетом (2.8) будет

(2.18)

Следуя (2.11) с учетом (2.18)

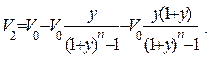(2.19)

Аналогично в соответствии с (2.17) для конца года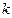

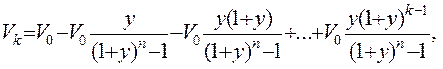(2.20)

или

Поскольку

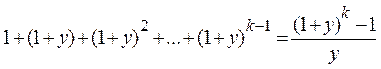
(2.21)

После приведения к общему знаменателю и деления числителя и знаменателя на получим

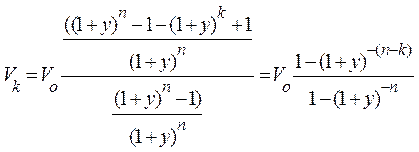
Обозначая

(2.22)

выражения для текущей стоимости актива записывают в виде

(2.23)

где 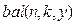называется функцией изменения стоимости актива во времени.

Дата добавления: 2014-01-05