Стоимость актива и земли с учетом бесконченой инфляции

В основу оценки стоимости положим формулу (5.9)

(6.30)

Дисконтирование (6.30) по темпу инфляции приводит к оценке стоимости

(6.31)

с учетом инфляции.

Введя обозначение

(6.32)

выражение (6.31) с учетом (6.30) перепишем так

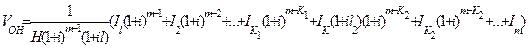(6.33)

После выполнения делений в (6.33) запишем

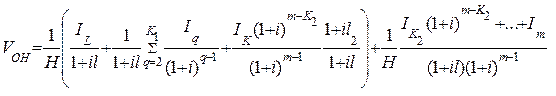(6.34)

Выражение (6.34) является общим для оценки стоимости недвижимости с учетом инфляции.

Выделим в нем реверсионную составляющую. Для этого умножим предварительно знаменатель выражения (последней составляющей в (6.34)).

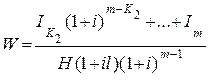(6.35)

на величину

Тогда с учетом (6.32) формула (6.35) будет

(6.36)

Денежный поток от реверсии обозначим так

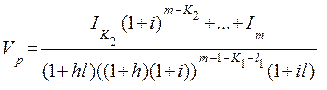(6.37)

Тогда будет

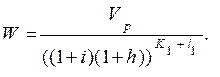(6.38)

А оценку объекта в соответствии с (6.34) определим так

(6.39)

Для вывода формулы оценки стоимости земли необходимо найти

Пусть за период чистый операционный доход (ЧОД) составил Его связь с годовым доходом можно выразить так

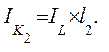(6.40)

Тогда

(6.41)

На дату 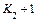ЧОД будет

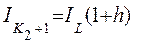(6.42)

на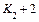

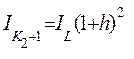(6.43)

а на дату

(6.44)

Найдем теперь сумму

(6.45)

С учетом (6.41) – (6.45) будем иметь

(6.46)

Найдем следующее слагаемое выражения (6.46)

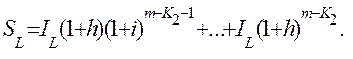(6.47)

Разделим выражение (6.47) на величину

Тогда получим

(6.48)

В выражении (6.48) сумма представляет собой сумму членов геометрической прогрессии с первым членом

(6.49)

и ее знаменателем

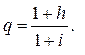(6.50)

Число членов геометрической прогрессии

Очевидно, что

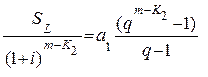(6.51)

с учетом (6.51) выражение (6.37) будет

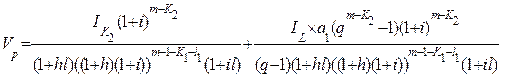(6.52)

После сокращений на с учетом (6.49) (6.50) выражение (6.52) запишем так

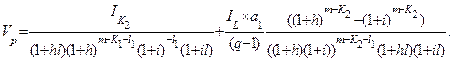(6.53)

Вторая составляющая этого выражения после почленного деления будет

(6.54)

При стремящемся к бесконечности как (6.54), так и первый член в (6.53) стремятся к нулю. Следовательно

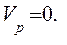
При стремящемся к бесконечности (6.32) также стремится к бесконечности. Тогда (6.34) будет полностью стремиться к нулю. Следовательно, при инфляции

Это значит, что в денежном выражении стоимость объектов недвижимости при инфляции нулевая, т.е. продавать объекты недвижимости при условиях инфляции нельзя, т.к. стоимость вырученных денег при этом стремится к нулю.

Данный вывод справедлив лишь при бесконечной инфляции. В случае же ограниченной во времени инфляции объект имеет конечную стоимость.

Дата добавления: 2014-01-05