Уравнения равновесия и их интегрирование. Основное уравнение гидростатики

Гидростатика – раздел гидромеханики, изучающий равновесие жидкости. Различают абсолютное равновесие жидкости, когда из массовых сил действует лишь сила тяжести, и относительное равновесие, когда на жидкость, кроме сил тяжести, действуют инерционные силы. В этом случае объем жидкости может двигаться, не деформируясь, как твердое тело, когда движение частиц друг относительно друга отсутствует.

В этом разделе будет рассмотрена гидростатика несжимаемой жидкости. В силу этого полученные выводы будут полностью справедливы только для практически несжимаемых капельных жидкостей. Для воздуха (газа) полученные зависимости можно применять, если разность высот в рассматриваемом объеме жидкости незначительны. В противном случае необходимо учитывать зависимость плотности от высоты места и температуры.

Связь между массовыми и поверхностными силами в жидкости, находящейся в равновесии, устанавливается уравнениями равновесия, для получения которых необходимо в формуле (1.21) ускорение жидкости приравнять нулю. Кроме этого необходимо учесть, что в покоящейся жидкости касательные напряжения равны нулю, а нормальные напряжения по условию (1.13) характеризуются давлениями.

Учитывая эти условия, можно из уравнения движения жидкости в напряжениях получить векторное уравнение равновесия жидкости

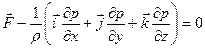. (2.1)

Рассмотрим наиболее часто используемый случай, когда на жидкость из массовых сил действует только сила тяжести . Напряжение этой силы, как было показано в п. 1.2, 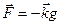. Тогда уравнение (2.1) примет вид

,

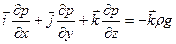проектируя которое на оси координат, можно получить систему трех скалярных уравнений равновесия жидкости

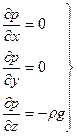(2.2)

Как видно из двух первых уравнений системы (2.2), давление зависит только от координаты z, и не зависит от изменения координат x и y. Отсюда следует, что если на покоящуюся жидкость действует только сила тяжести, то гидростатические давления в любой точке горизонтальной плоскости, мысленно проведенной в одной и той же жидкости, равны между собой. Такие горизонтальные плоскости называются поверхностями равного давления, одна из них изображена на рис.6.

На этом свойстве гидростатических давлений основан принцип сообщающихся сосудов, а также принцип работы жидкостных манометров.

Рис. 6

Так как в рассматриваемом случае изменение давления вдоль осей x и y отсутствует, то есть давление зависит только от координаты z, вместо системы (2.2) можно записать одно уравнение, заменив в нем частную производную на полную:

.

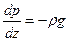Для того чтобы получить зависимость давления от координаты z, необходимо проинтегрировать это уравнение. Перепишем его в виде

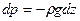
и проинтегрируем, учитывая, что :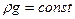

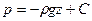, (2.3)

где C – произвольная постоянная интегрирования.

Для ее определения используем условие на свободной поверхности жидкости, на которой действует давление верхней среды (воздуха) p₀. Если совместить плоскость X0Y cо свободной поверхностью (рис.7), то получим условие

при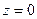

Подставляя эти значения в (2.3), получим значение константы интегрирования C=p₀. Тогда получим интеграл уравнения равновесия в окончательном виде

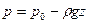. (2.4)

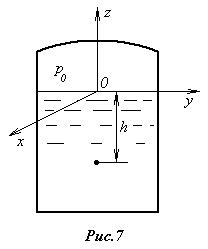Так как нас интересует давление в произвольной точке жидкости, распо-ложенной на определенной глубине под свободной поверхностью (рис.6), то удобнее Поль-зоваться уравнением (2.4) в виде

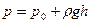(2.5)

Это уравнение назы-вается основным уравне-нием гидростатики, так как позволяет вычислить гид-ростатическое давление в любой точке жидкости. Здесь p – абсолютное давление в точке жидкости, p₀ – давление на свободной поверхности, rgh – давление столба жидкости высотой h.

Если сосуд открыт, то давление на свободной поверхности будет равно атмосферному (p_a), и формула (2.5) примет вид

.

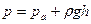В гидростатике используется понятие избыточного гидростатического давления, которое показывает, на сколько абсолютное давление больше атмосферного, т. е. . Если абсолютное давление меньше атмосферного, то вводят понятие вакуума – величины, которая показывает, на сколько измеряемое давление меньше атмосферного, т. е. .

Дата добавления: 2014-01-05