Сила гидростатического давления, действующая на плоскую стенку

Одним из важнейших практических приложений основного уравнения гидростатики является расчет сил, вызванных гидростатическим давлением, на различные поверхности.

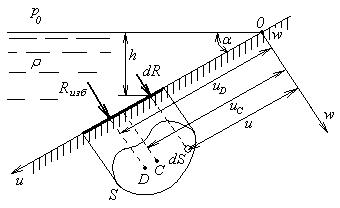Рис. 8

Выведем общие выражения для сил, действующих на плоскую стенку. Рассмотрим на плоской поверхности, расположенной под углом a к свободной поверхности жидкости (рис.8), участок произвольной формы, показанный жирной линией и имеющий площадь S. Оси координат выберем так, чтобы начало координат лежало в месте пересечения свободной поверхности жидкости с рассматриваемой наклонной поверхностью. Оси u и w связаны с наклонной поверхностью, как показано на рис.7. Для наглядности на рисунке рассматриваемый участок поверхности изображен также развернутым в плоскости чертежа.

Рассмотрим на участке S элементарную площадку dS и найдем действующую на нее силу суммарного давления

.

Чтобы найти силу, действующую на весь участок, надо предыдущее выражение проинтегрировать по всей площади S:

.

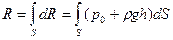Согласно рис.8, глубина 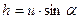, тогда

Величины p₀, r, g, sin a постоянны для всей поверхности S, поэтому можно записать

,

при этом интеграл во втором слагаемом представляет собой статический момент площади рассматриваемого участка относительно оси w, то есть

,

где u_c – координата центра тяжести площади S.

Осуществим обратный переход от координаты u к глубине h: 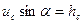и получим выражение для силы в виде

(2.6)

или .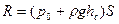

Для практики наибольший интерес представляет определение результирующей силы избыточного гидростатического давления 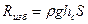. Определим точку ее приложения D, называемую центром давления и имеющую координату u_D. Момент силы избыточного давления, действующего на элементарный участок dS относительно оси w, равен

.

Тогда момент сил избыточного давления на всю поверхность S

.

Последний интеграл является моментом инерции площади относительно оси w, т. е. , то

. (2.7)

С другой стороны, если точка приложения силы избыточного давления D отстоит от оси w на величину u_D, то можно записать

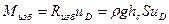. (2.8)

Приравнивая правые части уравнений (2.7) и (2.8) и учитывая, что , получим выражение для u_D:

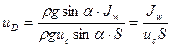. (2.9)

Переходя от момента инерции J_w относительно оси w к моменту инерции J_c относительно оси, проходящей через центр тяжести площади S параллельно оси w, по известной формуле вместо (2.9) окончательно получим

(2.10)

Из (2.10) видно, что точка приложения результирующей силы гидростатического давления D всегда лежит ниже центра тяжести C на величину (эта величина всегда положительна). Это является следствием того, что давление увеличивается с глубиной, следовательно, на нижнюю часть площади S всегда действует большее суммарное давление, чем на верхнюю.

Дата добавления: 2014-01-05