Методы изучения движения жидкости

Кинематика рассматривает общие свойства движения жидкости без выяснения причин его возникновения, то есть без учета сил. Из-за того, что в кинематике силы не учитываются, ее выводы одинаково справедливы как для реальной, так и для невязкой жидкости.

При движении твердого тела расстояние между двумя любыми его точками остается неизменным во все время движения. При движении жидкости – среды легко деформируемой – характер движения в значительной степени усложняется. Если при изучении движения твердого тела достаточно знать траектории движения трех его точек, то при изучении потока жидкости принципиально надо знать все о движении всех жидких частиц этого потока, взаимное расположение и скорости которых могут в общем случае все время меняться.

Рассмотрим два основных метода изучения движения жидкости. Первый из них называется методом Лагранжа. По этому методу изучение движения жидкости происходит с позиций механики материальной точки. Лагранж предложил находить траектории всех частиц жидкости изучаемого потока, рассматривая их как материальные точки. Таким образом, надо взять фиксированную частицу жидкости, которая в начальный момент времени t₀ находилась в точке с координатами x₀, y₀, z₀ (рис.12), и проследить, как меняется ее положение в пространстве в зависимости от времени. Для этого для рассматриваемой частицы нужно задать изменение координат с течением времени:

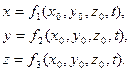
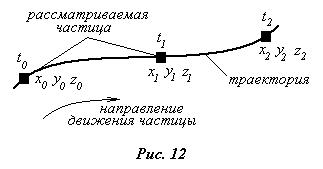
Если из этой системы уравнений исключить время, то получится уравнение траектории жидкой частицы, которая представляет собой путь, проделанный частицей в пространстве.

Первая производная по времени от проекций пути даст проекции скорости жидкой частицы

, , ,

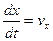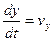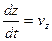а вторая производная - проекции ускорения

, , .

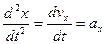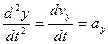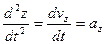Для того, чтобы изучить движении какого-либо объема жидкости, нужно знать элементы движений всех жидких частиц, входящих в этот объем. Но так как жидкий объем может быть подразделен на очень большое количество жидких частиц, становится ясной трудность применения данного метода к изучению движения жидкости. Кроме этого, в гидромеханике знание индивидуальных особенностей движения каждой жидкой частицы, как правило, не является необходимым. Все это приводит к тому, что метод Лагранжа применяется редко.

Значительно чаще используется другой метод изучения движения жидкости – метод Эйлера. Согласно этому методу, фиксируется внимание не на жидкой частице, а на точке пространства, через которую проходят жидкие частицы. Фиксируя скорости в разных точках пространства, заполненного жидкостью, можно получить так называемое поле скорости потока жидкости, то есть как бы мгновенную фотографию скоростей частиц жидкости во всех точках пространства. Под скоростью в точке пространства подразумевается скорость жидкой частицы, в данный момент времени занимающей эту точку. С течением времени жидкая частица, занимающая определенную точку пространства, покинет ее и освободит место для другой жидкой частицы. Таким образом, в соответствии с методом Эйлера, задается поле скорости жидкости во всех точках пространства, занятого ею. Если выбранная для наблюдения точка пространства имеет координаты x,y,z, (не путать с координатами x,y,z, определяющими положение частицы в методе Лагранжа), то скорости жидких частиц, проходящих через эту точку, в общем случае могут менять величину и направление, то есть движение будет неустановившимся и проекции скорости в точке будут равны

, , .

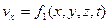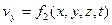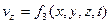В случае установившегося движения время из предыдущих формул исключается:

, , .

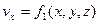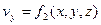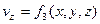Производная от скорости по времени даст ускорение жидкости в рассматриваемой точке:

, , .

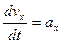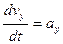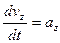Дата добавления: 2014-01-05