Линия тока и ее свойства. Критические точки

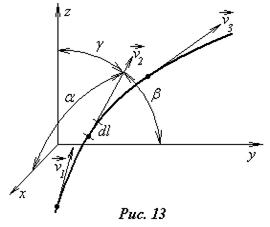Если для метода Лагранжа характерной является траектория жидкой частицы, то в методе Эйлера используется понятие линии тока. Кривая, в каждой точке которой вектор скорости совпадает с касательной к ней, называется линией тока (рис.13). Вообще в движущейся жидкости можно провести неограниченное количество линий тока, образующих се-мейство линий тока, положение которых в прост-ранстве в случае неустановившего-ся движения все время меняется. Если движение установившееся, то положение ли-ний тока не меняется в пространстве и они совпадают с траекториями жидких частиц.

Получим уравнение семейства линий тока. Возьмем на линии тока произвольную точку, где скорость частицы равна v, а ее проекции на оси координат, соответственно, v_x, v_y, v_z, и обозначим углы между вектором скорости и осями координат через a, b, и g. Тогда можно записать, что

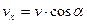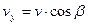, , . (3.1)

С другой стороны, для касательной к кривой в этой же точке по формулам аналитической геометрии

, , , (3.2)

где dl – элемент касательной в рассматриваемой точке, dx, dy, dz – его проекции на оси. Подставляя значения косинусов из выражений (3.1) в уравнения (3.2), можно получить

, , .

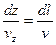В этих равенствах правые части равны, значит

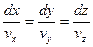. (3.3)

Зависимость (3.3) является дифференциальным уравнением семейства линий тока. При интегрировании этого дифференциального уравнения возникает константа интегрирования. Выбор этой константы и определяет конкретную линию тока.

Покажем, что линии тока в общем случае не могут пересекаться. Предположим, что это не так, и две линии тока пересекаются (рис.14). Тогда, по определению линии тока, жидкая частица в точке их пересечения будет иметь две скорости (одна касательная к одной линии тока –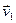, другая – ко второй – ). Если их сложить по правилу параллелограмма, то полученная результирующая скорость 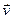не будет направлена по касательной ни к одной из линий тока, чего быть не может, так как частица лежит на линии тока и ее скорость должна быть направлена по касательной к ней. Следовательно, линии тока не пересекаются.

В ряде случаев возможен особый вариант, когда возникает пересечение линий тока. Рассмотрим установившееся обтекание симметричного тела (например, крыла) потоком жидкости, направленным вдоль плоскости симметрии (рис.15). Каждой линии тока над крылом соответствует симметричная ей линия тока под крылом (они обозначены на рисунке одинаковыми цифрами). Но всегда есть линия тока, не имеющая симметричной (обозначена цифрой 0), которая приходит в носик тела, затем разветвляется на две линии, идущие по поверхности тела, а в корме снова сливается в одну. Таким образом, в двух точках на теле пересекается по три линии тока, чего не может быть, если жидкая частица имеет скорость. Значит, в рассматриваемых точках, которые называются 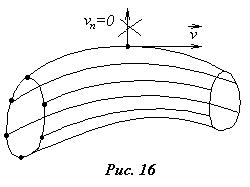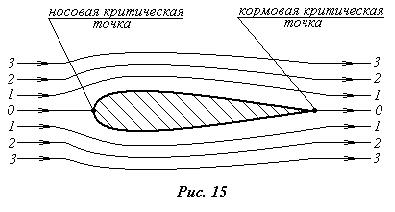критическими, скорость жидкой частицы равна нулю.

Рассмотрим еще одно свойство линий тока. Проведем мысленно в потоке жидкости замкнутый контур, не совпадающий с линией тока (рис.16). Через каждую точку этого контура про-ходят линии тока, которые в совокуп-ности образуют поверхность, назы-ваемую трубкой тока. Жидкость, находящаяся внутри трубки тока, называется жидкой струйкой. Так как поверхность трубки тока образована линиями тока, в каждой точке которых скорость касательна к ним, то есть нормальная составляющая скорости 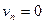, жидкость не может перетекать через стенку трубки тока и, следовательно, жидкая струйка состоит из одних и тех же частиц.

Дата добавления: 2014-01-05