Уравнение неразрывности. Расход

Классификация потоков жидкости.

Рассмотрим наиболее общий случай движения жидкости – пространственное неустановившееся движение. Это движение характеризуется тем, что скорость движения жидкости в каждой точке пространства является функцией четырех переменных – трех координат и времени

.

Наряду с общим случаем движения жидкости выделяется несколько других видов движения.

1. Установившееся движение жидкости – это такое движение, при котором скорость жидкости в фиксированной точке не изменяется во времени, то есть скорость зависит только от координат точки пространства

,

если же скорость зависит от времени, то движение называется неустановившимся.

2. Плоскопараллельное или двумерное течение жидкости – это течение, при котором в любом сечении, перпендикулярном некоторой оси, движение жидкости одинаково. Такое течение в чистом виде практически не встречается, но в некоторых случаях пространственное движение может быть сведено к плоскопараллельному. Например, при поперечном обтекании длинного цилиндра (рис.17), в сечениях А и В, а также в любых параллельных им сечениях, удаленных от концов цилиндра, течение жидкости будет одинаковым и не зависящим от переменной x. При этом можно ограничиться рассмотрением течения жидкости только в одном из этих сечений, т. е. на плоскости yz. Скорость в этом случае будет зависеть только от двух координат и времени

.

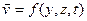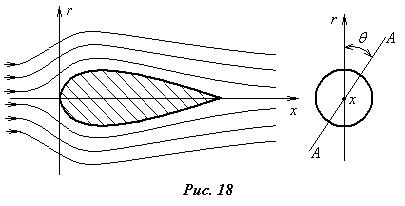
3.Осесимметричное движение жидкости, которым называется движение, имеющее ось симметрии (ось x на рис.18). Оно образуется при движении жидкости в трубах круглого сечения или при обтекании тел вращения. Такое движение удобно представлять в цилиндрической системе координат x,r,q. В силу того, что течение имеет ось симметрии, картина течения в любой плоскости (А-А), проходящей через ось симметрии, будет одинаковой и не зависящей от переменной q:

.

Все три выделенные вида течения жидкости отличаются от общего случая трехмерного неустановившегося движения тем, что в каждом из них скорость является функцией только трех переменных. Это значительно облегчает расчет таких течений, в силу чего они очень часто используются при решении различных теоретических и практических задач.

Любое движение жидкости должно удовлетворять закону сохранения материи (массы). Применительно к движущейся жидкости этот закон выражается уравнениями неразрывности. В общем случае закон сохранения материи имеет вид

,

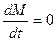где М – масса рассматриваемого объема жидкости V. Так как масса M=rV, закон сохранения материи для однородной жидкости, когда r=const, принимает форму

или , (3.3)

то есть для однородной несжимаемой жидкости закон сохранения массы переходит в закон сохранения объема.

Введем понятие расхода жидкости. Расходом Q называется количество жидкости, протекающее через поверхность в единицу времени. Расход может быть объемным Q_V и массовым Q_m. Объемный расход измеряется в м³/с, а массовый – в кг/с,

.

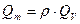Понятие объемного расхода используется для формулировки уравнения неразрывности, которое имеет три основных формы: интегральную, гидравлическую и дифференциальную.

А). Интегральная форма уравнения неразрывности. Для ее получения мысленно поместим в поток движущейся жидкости поверхность площадью S (рис.19), на которой выделим элементарную площадку dS. Скорость 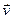жидкости в месте расположения площадки dS, может быть разложена на нормальную составляющую v_n и касательную составляющую v_t. Перенос жидкости через площадку dS может осуществляться только за счет нормальной составляющей скорости. При этом объемный расход жидкости через площадку dS

.

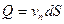Объемный расход жидкости, протекающей через всю поверхность S, равен

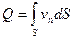. (3.4)

Расход жидкости через замкнутую поверхность, в соответствии с законом сохранения объема (3.3), равен нулю, так как количество втекающей жидкости должно быть равно количеству вытекающей жидкости, т. е.

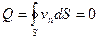, (3.5)

где кружок на знаке интеграла означает замкнутую поверхность.

Выражение (3.5) называется интегральной формой уравнения неразрывности.

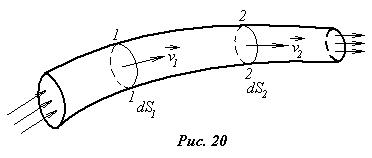
Б). Гидравлическая форма уравнения неразрывности. Рассмотрим участок элементарной жидкой струйки (жидкой струйки с малым поперечным сечением), показанной на рис.20, и выделим в ней два сечении, перпендикулярные линиям тока, которые называются живыми сечениями 1-1 и 2-2, с площадями dS₁ и dS₂ соответственно. Ввиду малости сечения жидкой струйки можно считать скорости в каждой точке сечения одинаковыми и равными в рассматриваемых сечениях v₁ и v₂ соответственно. Объемный расход в первом сечении , а во втором . Так как через боковую поверхность жидкой струйки перетекания жидкости нет (по определению жидкой струйки на боковой поверхности 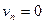), то вся жидкость из сечения 1-1 перейдет в сечение 2-2, то есть 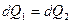или . Сечения 1-1 и 2-2 были выбраны совершенно произвольно, поэтому можно считать, что вдоль жидкой струйки расход остается постоянным

.

Теперь рассмотрим поток конечных размеров, ограниченный твердыми стенками (рис.21). Из-за конечности размеров потока скорости в каждом живом сечении (1-1) и (2-2) нельзя считать постоянными, в связи с чем расход в сечениях определяется по формуле (3.4)

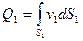, и .

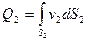Так как через твердые стенки, так же как и через линии тока, нет перетекания жидкости, то .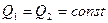

Введем понятие средней скорости, которой называется условная постоянная по сечению скорость, дающая расход, равный действительному. На рис.22 показано действительное распределение скоростей по сечению потока и средняя скорость.

Из определения средней скорости следует, что

.

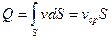Тогда и , а так как и здесь сечения выбирались произ-вольно, то уравнение неразрывности в гидравлической форме можно записать в виде

. (3.6)

Таким образом, при движении несжимаемой жидкости по трубам, уменьшение площади поперечного сечения потока приводит к увеличению его средней скорости, и наоборот.

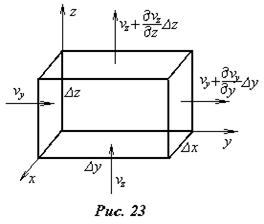В). Дифференциальная форма уравнения неразрывности. Поместим мысленно в поток движущейся жидкости неподвижную систему координат и связанную с ней замкнутую поверхность в виде элементарного прямоугольного параллелепипеда со сторонами Dx, Dy, Dz (рис.23), через который протекает жидкость. Подсчи-таем расход жид-кости через выбранную по-верхность. Нор-мальная скорость к площадке 12341 в выбранной системе координат v_n=v_z и элементарный рас-ход через эту грань Q₁₂₃₄₁=v_zDxDy. Нормальная составляющая скорости через противоположную грань 56785 в общем случае не равна v_z и может быть представлена в виде 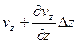, а расход через нее 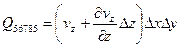. Условимся за положительное считать направление, совпадающее с внешней нормалью к поверхности по отношению к объему, ограниченному этой поверхностью. Тогда общий расход через две рассмотренные поверхности

Соответственно через каждую пару оставшихся граней расход равен

, .

Так как в силу закона сохранения объема (3.3) общий расход жидкости через рассматриваемую замкнутую поверхность параллелепипеда должен быть равен нулю, то

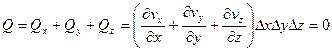
Так как объем параллелепипеда DV=DxDyDz ¹0, то полученное равенство можно на него разделить и получить уравнение неразрывности в дифференциальной форме

(3.7)

Дата добавления: 2014-01-05