Ускорение жидкой частицы

Получим выражение для ускорения жидкой частицы, задавая движение жидкости по методу Эйлера, когда известно поле скоростей.

Ускорение жидкой частицы 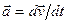. Так как скорость является сложной функцией координат частицы и времени , то, по правилу дифференцирования сложных функций, получим

.

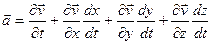Учитывая, что для движущейся частицы

, , ,

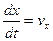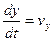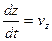выражение для ускорения можно переписать в виде

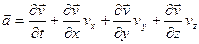. (3.8)

Как видно из (3.8), ускорение жидкой частицы складывается из двух частей: первое слагаемое, непосредственно зависящее от времени, называется местным или локальным ускорением, а последние три слагаемых называются конвективным ускорением.

Местное ускорение – это результат изменения с течением времени скорости в фиксированных точках пространства, т. е. когда движение жидкости неустановившееся. Символ частной производной означает, что при ее вычислении координаты точек считаются неизменными. При установившемся движении местное ускорение .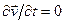

Возникновение конвективного ускорения 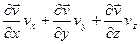обусловливается тем, что в разных точках пространства скорости жидкости различны. Поэтому конвективное ускорение, а, следовательно, и полное ускорение в установившемся течении не равно нулю. Лишь в одном частном случае однородного поля скоростей, когда 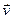не зависит от координат, конвективное ускорение равно нулю.

Проектируя (3.8) на оси координат, получим три скалярных уравнения для проекций ускорения

,

, (3.9)

.

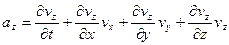Поясним значение локального и конвективного ускорений на примере трубы с переменным поперечным сечением (рис.24). По трубе течет жидкость с постоянным расходом Q. Следуя методу Эйлера, рассмотрим скорости в точках, лежащих на оси трубы. В каждой из рассматриваемых точек скорость, величина которой определяется расходом и сечением трубы, постоянна по времени (так как Q=const), то есть движение установившееся. При этом в том месте, где сечение трубы уменьшается, скорость потока увеличивается, и, наоборот, при увеличении сечения скорость уменьшается (3.6). Таким образом, из сечения 1-1 частица будет перемещаться вдоль оси трубы в область, где сечение трубы уменьшается, следовательно, ее скорость будет увеличиваться. Значит, при переносе частицы потоком от сечения 1-1 до сечения 2-2 ее скорость будет увеличиваться, что говорит о наличии на этом участке положительного конвективного ускорения. Рассуждая аналогичным образом, можно показать, что в сечении 2-2 конвективное ускорение равно нулю, а на участке между сечениями 2-2 и 3-3 оно меньше нуля.

Дата добавления: 2014-01-05