Истечение жидкости из отверстий и насадков

Одной из практически важных задач, рассматриваемых в курсе гидравлики, является расчет истечения жидкости из отверстий. Особенность этой задачи состоит в том, что поток жидкости является очень коротким и поэтому можно пренебречь потерями на трение, так как они малы по сравнению с местными потерями, возникающими на выходе из отверстия.

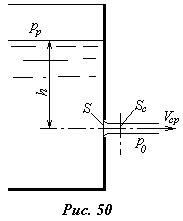1). Истечение жидкости в атмосферу. Рассмотрим истечение жидкости из отверстия в тонкой стенке резервуара в окружающую атмосферу (рис.50). Наблюдения показывают, что вытекающая из такого отверстия струя сжимается, и площадь S_с ее живого сечения после выхода из отверстия становится меньше площади отверстия S. Сжатие струи обусловлено действием сил инерции, возникающих в струе при огибании жидкостью кромок отверстия. Особенно сильно огибание кромок сказывается на частицах, траектории которых находятся под углами, близкими к 90⁰ относительно оси отверстия, т. е. движущихся вдоль стенок. Степень сжатия определяется коэффициентом сжатия струи e=S_c/S. Величина этого коэффициента зависит от формы и абсолютных размеров отверстия, от скорости истечения, а также, в случае отверстия в вертикальной стенке, от расположения отверстия относительно дна сосуда. Если отверстие находится рядом с дном (на расстоянии меньше трех диаметров отверстия), то со стороны дна сжатия струи не будет, или оно будет частичным. В случае отсутствия влияния дна или других поперечных стенок на истечение из отверстия коэффициент сжатия для круглых и квадратных отверстий составляет e =0.60¸0.64.

Вычислим скорость течения жидкости в струе, если на поверхности жидкости в резервуаре давление p_p не равно атмосферному p₀, куда вытекает струя. Глубина погружения отверстия под свободной поверхностью жидкости равна h. Течение в струе после ее выхода можно считать плавно изменяющимся. Применим уравнение Бернулли к сечениям потока, первое из которых совпадает со свободной поверхностью жидкости в резервуаре, а второе – с живым сечением струи сразу после ее выхода из отверстия. Пренебрегая потерями на трение жидкости о стенки резервуара, получим

.

Последнее слагаемое учитывает местную потерю на выходе из отверстия.

Скорость опускания уровня в резервуаре V_{ср р} будем считать малой. Это возможно только тогда, когда площадь отверстия S значительно меньше площади свободной поверхности жидкости в резервуаре S_p, тогда квадратом скорости в первом слагаемом уравнения Бернулли можно пренебречь. С учетом этого для средней скорости истечения жидкости из отверстия получим выражение

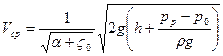. (5.25)

Теперь определим расход Q жидкости при истечении из отверстия

.

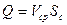Подставляя сюда величину средней скорости из (5.25), и выражая площадь сечения струи S_c через площадь отверстия, находим

. (5.26)

Величина

(5.27)

называется коэффициентом расхода данного отверстия. Таким образом, можно записать окончательно

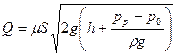. (5.28)

Значения коэффициента расхода определяются экспериментально. Для небольших круглых и квадратных отверстий в среднем m =0.62, для более крупных отверстий m =0.65¸0.70. При наличии влияния стенок коэффициент расхода увеличивается, а по мере увеличения напора h он уменьшается.

2). Истечение через затопленное отверстие. Для судостроения представляет интерес случай истечения через затопленное отверстие, т. е. перетекание из одной заполненной емкости в другую, которая заполнена частично (рис.51). При таком истечении происходит сжатие струи с последующим ее расширением. В связи с этим, кроме потерь энергии на выходе из отверстия, следует учитывать также потери вследствие внезапного расширения струи.

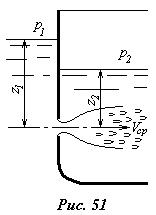Проведем плоскость сравнения через ось отверстия, полагая изменения высот уровня жидкости слева и справа от отверстия малыми и пренебрегая их квадратами, запишем уравнение Бернулли для сечений, расположенных на свободной поверхности. Учитывая при этом местные потери энергии в отверстии, получим

,

откуда .

Коэффициент расширения z_р в данном случае практически равен единице. С учетом этого расход жидкости через затопленное отверстие

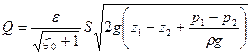. (5.29)

Коэффициент расхода затопленного отверстия

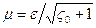
близок по величине к коэффициенту незатопленного отверстия, так как в (5.27) можно положить a»1.

3). Истечение через насадки. Для увеличения расхода жидкости и создания направленной струи к отверстию приставляют трубки небольшой длины, которые называются насадками. Насадки могут быть различной формы (рис.52) – цилиндрические – I и II, конические – сходящиеся и расходящиеся - III и IV, коноидальные V. Кроме того, они делятся на внутренние II и III и внешние I IV, V. При правильном режиме работы насадка живое сечение выходящей через него струи равно площади выходного сечения насадка. При этом устраняется сжатие струи на выходе из насадка, и коэффициент сжатия струи на выходе e =1. В этом состоит основное свойство насадка.

Рассмотрим принцип действия цилиндрического внешнего насадка (рис.53). Струя, входящая в насадок, сначала сжимается, аналогично выходу из отверстия. Однако в дальнейшем струя расширяется, и на некотором расстоянии от входа занимает все сечение насадка. Воздух, заключенный в пространстве между сжатой струей и стенками насадка, уносится потоком воды, и в этом промежутке, то есть в сжатом сечении, на поверхности жидкости образуется вакуум – разрежение. В результате вакуума увеличивается перепад давления между свобод-ной поверхностью жид-кости и сжатой струей по сравнению с имею-щим место при исте-чении жидкости из простого отверстия. Это вызывает, согласно уравнению Бернулли, возрастание скорости в сжатом сечении в насадке – насадок как бы сосет воду. Однако в насадке увеличиваются и потери энергии. Во-первых, за счет потерь на расширение струи в насадке, во-вторых, за счет потерь на трение жидкости о стенки насадка. При правильной конструкции насадка влияние этих возросших потерь должно компенсироваться эффектом засасывания, в результате чего расход насадка должен быть больше расхода отверстия.

Средняя скорость на выходе из насадка получается путем применения уравнения Бернулли для сечения на поверхности воды в баке и для сжатого сечения в насадке. Проведя преобразования, аналогичные проделанным для истечения жидкости из отверстия, получим формулу

,

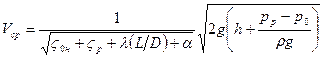где z_0н – коэффициент местных потерь на вход в насадок, z_р - коэффициент местных потерь при расширении струи, l - коэффициент потерь на трение в насадке.

Расход воды в насадке, с учетом того, что e =1, будет

.

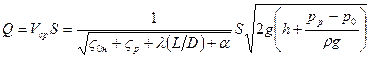Коэффициент расхода насадка

должен быть больше коэффициента расхода отверстия (5.25), то есть

.

Это условие можно свести к более простому соотношению, дающему геометрические параметры насадка

.

В соответствии с этим условием предельная длина насадка в зависимости от коэффициента сопротивления l

L =(40¸50) D.

При длине насадков L =(3¸4) D их коэффициент расхода m»0.82. В насадках меньшей длины возможен прорыв воздуха извне в зону вакуума; при этом струя в насадке не сможет расшириться и коэффициент расхода резко уменьшится.

Максимальный коэффициент расхода m =0.95 имеют конические сходящиеся насадки с углом конусности 13⁰. Для расходящихся насадков характерно наибольшее разрежение в сжатом сечении, такие насадки применяют в тех случаях, когда нужно обеспечить большой расход жидкости при небольших скоростях на выходе из насадка.

Дата добавления: 2014-01-05