Расчет времени опорожнения отсеков

Еще одной важной практической задачей гидравлики является определение времени опускания уровня жидкости в резервуаре до заданной отметки при ее истечении из отверстия или насадка. Определение этого времени связано с необходимостью решения задачи о времени опорожнения отсеков или выравнивания уровня жидкости в сообщающихся резервуарах.

Строго говоря, решение этой задачи требует применения уравнения Бернулли для неустановившегося течения вязкой жидкости. Однако, если считать что скорости изменения уровня жидкости, а следовательно и местные ускорения частиц 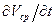малы, можно пренебречь влиянием этих ускорений на процесс истечения. В этом случае можно пользоваться уравнением Бернулли для установившегося течения жидкости (5.14) и определять мгновенные значения расходов Q по формулам, полученным в предыдущем разделе.

Рассмотрим случай, когда требуется определить время, в течение которого жидкость будет опускаться в резервуаре произвольной формы от начального своего уровня h₀ до заданной отметки h₁ (рис. 54). Истечение может происходить через отверстие или из насадка. Предпо-лагается, что давле-ния на поверхности жидкости в резер-вуаре p_р и на по-верхности вытека-ющей струи p₀ неодинаковы. Для определения мгно-венного значения расхода жидкости, вытекающей из отверстия, воспользуемся формулой (5.28)

,

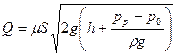полагая в ней h равным мгновенной высоте уровня жидкости над центром отверстия.

В соответствии с этой формулой элементарный объем жидкости, вытекший за время dt через отверстие, составит Qdt. Вызываемое этим уменьшение объема жидкости в резервуаре равно произведению площади свободной поверхности на изменение напора –dh, то есть

.

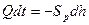Подставив сюда значение расхода Q, получим

,

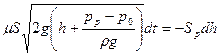откуда время опускания уровня жидкости от h₀ до h₁ определится интегрированием

.

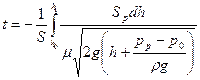Следует учесть, что в общем случае резервуара произвольной формы площадь его свободной поверхности S_p является функцией от h, коэффициент расхода m также зависит от величины мгновенного напора h. Однако m можно практически считать постоянной величиной. С учетом этого можно записать

. (5.30)

Входящий в формулу (5.30) интеграл может быть в случае отсека произвольной формы рассчитан по правилам приближенного интегрирования (например, по правилу трапеций).

В частном случае, когда S_p(h)=S_p=const, можно найти этот интеграл:

,

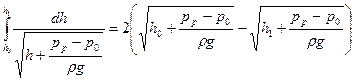т. е. 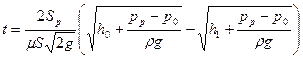. (5.31)

Полагая в (5.30) и (5.31) h₁ =0, можно найти время полного опорожнения резервуара. Нетрудно заметить, что эти формулы дают также решение задачи о повышении уровня от h₀ до h₁ в сосуде, сообщающимся с другим резервуаром, где высота уровня жидкости, относительно которого измеряются h₀ и h₁, предполагается постоянной. Это соответствует задаче о затоплении отсека судна.

Список литературы

1. Фаддеев Ю.И., Чехович А.Г. Гидромеханика. Учебное пособие для вечернего и заочного факультетов.// Изд. ЛКИ, 1975.

2. Войткунский Я.И., Фаддеев Ю.И., Федяевский К.К. Гидромеханика.// Л., Судостроение, 1968 (первое издание).

3. Амфилохиев В.Б., Золотов С.С., Фаддеев Ю.И. Задачник по гидромеханике для судостроителей.// Л., Судостроение, 1984.

Дата добавления: 2014-01-05