Спектральный анализ оптических сигналов

Спектр периодического сигнала, последовательность прямоугольных импульсов, ее спектр амплитуд и форма огибающей спектра. Непериодические сигналы, спектр непериодического сигнала, понятие прямого и обратного преобразования Фурье, запись преобразования Фурье в комплексной форме.

Тема 5. Тема 6. Спектральный анализ оптических сигналов. Понятие периодического процесса, гармоническое колебание и его аналитическая запись, форма и параметры (амплитуда, частота, начальная и полная фазы колебания). Сложный периодический процесс и его представление рядом Фурье. Понятие о спектре амплитуд и спектре фаз. Периодические сигналы их свойства.

Законы теплового излучения

(см. лабораторную работу «Исследование излучения нагретых тел»)

Используется с целью определения распределения энергии сигнала по частотному диапазону.

Известно из курса физики, что белый свет представляет собой сложное электромагнитное колебание, которое с помощью призмы можно разложить на отдельные спектральные составляющие показывающие его качественный состав. По аналогии с этим можно сложное звуковое колебание представить в виде набора гармонических колебаний звуковой частоты, а любой сложный процесс представить состоящим из отдельных гармонических колебаний. Основой такого представления является широко используемый в технике гармонический анализ процессов, выполняемый с помощью математического аппарата разложения Фурье. Широкое распространение гармонического анализа обусловлено свойствами гармонического колебания: оно является простейшей функцией неподдающейся дальнейшему разложению, сохраняет свою форму при прохождении через любую линейную систему. Аналитически, гармоническое колебание, действующее на временном интервале -¥<t<+¥, может иметь несколько видов записи

u(t)=UCos[2π(t/T)-y]=UCos(wt-y)=UCosj, (1)

где U- амплитуда колебания, T-период колебания, w=2πf - круговая частота колебания, f - циклическая частота, y,j - начальная и полная фазы колебания,

либо в виде действительной, или мнимой части комплексной переменной.

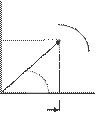
u(t)=URe[e^jj], так как e^jj=Cosj+jSinj, то u(t)=URe[Cosj+jSinj]=UCosj, либо u(t)=UIm[Cosj+jSinj]=USinj.

Im   w     j   Re u(t)

Графически гармоническое колебание представляется в виде вращающегося с угловой скоростью w вектора u в комплексной плоскости, либо периодически меняющегося во времени сигнала u(t). Периодическим считается процесс, отражающий бесконечное повторение одного и того же события, т.е. если для любого момента времени u(t)= u(t+T), где T- некоторая константа.

Для одномерного пространственного гармонического колебания на интервале -¥<x<+¥ аналитическая запись может быть представлена в виде u(x)=Acos[(2π/l)-y]=Acos(px-y)=ACosj, где

p=2πn=2π/l - пространственная круговая частота, а n - циклическая пространственная частота.

Дата добавления: 2014-01-05