Поток векторного поля через поверхность

МАТЕМАТИЧЕСКОЕ ОТСТУПЛЕНИЕ

Лекция 2. Потенциал электростатического поля.

Работа электростатического поля при перемещении зарядов. Циркуляция вектора напряжённости. Связь напряжённости и потенциала.

Будем предполагать, что в некоторой области пространства задано непрерывно-дифференцируемое векторное поле .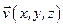

Потоком вектора 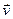через некоторую поверхность называется величина .

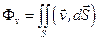В простейшем случае плоской поверхности S и однородного векторного поля поток определяется как

,

где a - угол между вектором 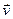и нормалью 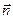к площадке S.

Если поверхность S не является плоской, то она разбивается на элементарные участки величиной dS, такие, что каждый из них можно рассматривать как малую часть плоскости, а поле вблизи площадки – постоянным. Затем для каждого из участков ищется соответствующая величина 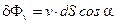, а потом производится суммирование по всей поверхности .

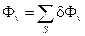Если ввести вектор, перпендикулярный к каждой площадке: , где 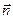- единичная нормаль к площадке dS, то величину потока записать можно в виде .

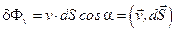Тогда общий поток .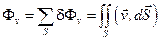

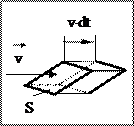Пример. Найдем объем жидкости протекающей через некоторую малую наклонную площадку за единицу времени.

Пусть скорость жидкости равна v и в пределах площадки её можно считать постоянной, тогда объём жидкости, прошедшей через площадку за малый промежуток времени dt, заполнит внутренность косого параллелепипеда, объём которого равен 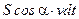. Здесь a - угол отклонения вектора скорости жидкости 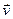от направления, перпендикулярного площадке, т.е. угол между вектором единичной нормали к площадке и вектором скорости жидкости. Если ввести вектор 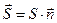, то объёмный расход жидкости, т.е. объём жидкости, протекающей через площадку в единицу времени, можно определить соотношением .§

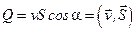2) Циркуляция векторного поля.

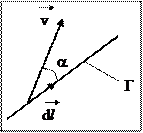
Рассмотрим интеграл от векторного поля вдоль кривой линии Г: , где 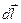- касательный вектор к каждой точке кривой. Таким образом, кривая является ориентированной – она имеет начальную и конечную точки (так как задано направление вдоль кривой с помощью вектора ).

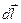В случае, когда векторное поле постоянное, а кривая – отрезок прямой линии длиной L, интеграл равен

,

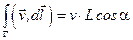где a - угол между векторами поля и касательным вектором.

В случае если кривая линия не является прямой и векторное поле не постоянное, нужно разбить линию на малые (почти) прямолинейные участки длиной dl, такие, что на каждом из участков поле можно рассматривать как постоянное. Для каждого участка найти величину , а затем просуммировать полученные все выражения

.

Пусть кривая линия является замкнутой (без самопересечений во внутренних точках). Такую линию будем в дальнейшем называть контуром. Интеграл от векторного поля 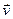по замкнутой кривой Г: называется циркуляцией этого векторного поля вдоль контура Г.

Дата добавления: 2014-01-05