Теорема Стокса

Если рассмотреть незамкнутую поверхность S, то край этой поверхности будет являться замкнутой кривой. Будем считать, что поверхность является ориентируемой (т.е. она – двусторонняя). Если Г – кривая, являющаяся краем поверхности S, то можно рассмотреть циркуляцию векторного поля вдоль края Г: .

Векторному полю 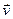можно сопоставить ещё одно векторное поле 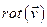, которое называется ротором векторного поля 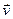. В декартовой системе координат оно определяется соотношением

,

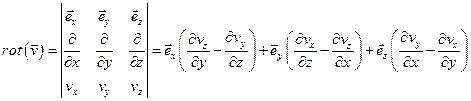где 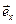, , 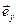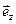- орты декартовой системы координат.

Теорема Стокса гласит:

.

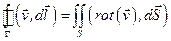Циркуляция векторного поля вдоль края ориентируемой поверхности равна потоку ротора этого поля через эту поверхность. Направление касательного вектора 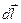к краю Г выбирается так чтобы поверхность оставалась слева при обходе, а нормаль направлена наружу (правый винт).

Смысл ротора можно прояснить следующим примером. Рассмотрим диск, вращающийся вокруг оси симметрии с угловой скоростью w. Скорость любой точки определяется расстоянием до оси вращения 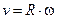. Вектор скорости любой точки направлен по касательной к её траектории – окружности с центром на оси вращения. Можно сказать, что на диске задано векторное поле – поле векторов скоростей всех точек 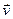. Найдем ротор этого поля 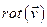. Воспользуемся теоремой Стокса

.

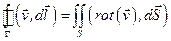Если взять малую площадку S, то по теореме о среднем для интеграла можно приближенно записать 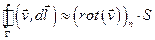, где 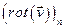- проекция ротора на нормаль к площадке S.

В качестве кривой Г возьмём окружность малого радиуса R с центром на оси вращения. Длина этой окружности 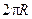, она охватывает площадку S, площадь которой .

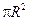В каждой точке этой окружности вектор скорости направлен по касательной к ней, поэтому угол между малым касательным вектором 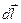и вектором скорости 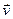равен нулю. Следовательно

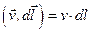
На выбранной окружности Г величина скорости не меняется 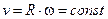. Тогда

.

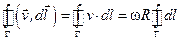Интеграл 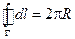равен длине окружности Г, поэтому циркуляция .

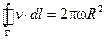Откуда

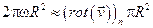
После сокращений устремим радиус окружности R к нулю, и получим проекцию ротора на ось вращения

.

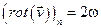Т.е. ротор векторного равен удвоенной угловой скорости вращения точек области, где задано векторное поле. Поэтому иногда ротор также называют вихрем поля. Поля, для которых ротор отличен от нуля называют вихревыми или соленоидальными. Оказывается, для любого вихревого поля 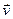существует некоторое векторное поле 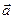, такое, что выполняется равенство .

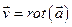4) Векторное поле 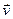, для которого существует непрерывно-дифференцируемая функция Ф такая, что выполняется равенство

,

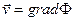называется потенциальным.

Ротор потенциального поля равен нулевому вектору .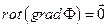

Действительно, т.к. 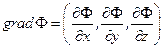, то

.

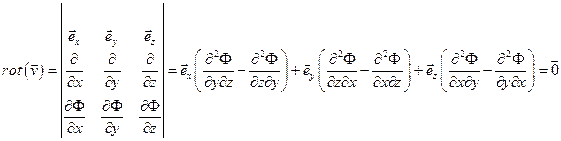Дата добавления: 2014-01-05