Теория Бора

Попытку снять это противоречие предпринял Нильс Бор в 1913 г. Для этого он предположил, что существуют состояния атома, в которых электрон движется по определённым орбитам, не излучая электромагнитные волны. Такие состояния он назвал стационарными. При переходе из одного стационарного состояния в другое атом излучает или поглощает квант энергии:

.

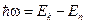Эти предположения получили название постулаты Бора.

В теории Бора возможны только такие орбиты, для которых момент импульса электрона кратен постоянной ħ: .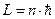

Учитывая, что в этой модели орбиты являются круговыми, поэтому для момента импульса электрона можно записать выражение: 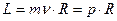, получаем, что условие 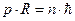эквивалентно 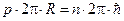, т.е. 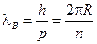- на орбите укладывается целое число длин волн де Бройля для электрона.

Спектр излучения атома водорода к тому времени уже был достаточно хорошо изучен. Для циклической частоты излучения опытные данные давали (обобщенную) формулу Бальмера:

,

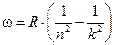где R – постоянная Ридберга, n, k – натуральные числа, .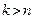

К достоинствам модели атома Бора можно отнести тот факт, что эта модель позволила объяснить, в частности, эту формулу.

Рассмотрим модель атома, в котором лёгкий электрон движется по круговой орбите радиуса R вокруг тяжёлого положительно заряженного ядра (Z – зарядовое число):

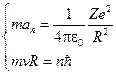или , .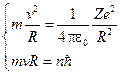

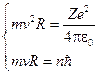Откуда для скорости электрона получаем: 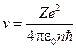, и радиус орбиты:

.

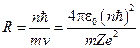Полная механическая энергия системы равна сумме кинетической и потенциальной энергий:

.

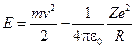Т.к. из уравнения движения следует равенств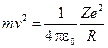о: , то .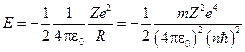

Следовательно, энергия электрона в атоме определяется выражением:

.

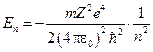Число n определяет значение энергии электрона и называется главным квантовым числом.

Для атома водорода Z =1, поэтому 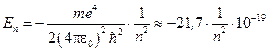Дж или

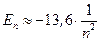эВ. Следовательно, для отрыва электрона от атома (ионизации атома) водорода необходима энергия 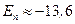эВ.

Первый Боровский радиус:

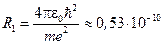м

– радиус самой «низкой» орбиты электрона по порядку величины совпадает со средним размером атома, полученным экспериментально. Первый Боровский радиус соответствует невозбуждённому (основному) состоянию атома.

Состояниям с большей энергией соответствуют большие радиусы орбит.

При переходе из одного стационарного состояния в другое энергия кванта излучения равна, :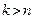

.

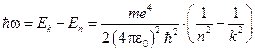Для круговой частоты получаем обобщённую формулу Бальмера: ,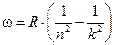

где постоянная Ридберга 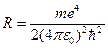. Стоит отметить, что её значение хорошо согласуется с экспериментальным значением: 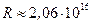с^-1.

Замечание. При излучении или поглощении кванта меняется энергия атома, следовательно, меняется главное квантовое число n. При изменении главного квантового числа меняется момент импульса атома, следовательно, в соответствии с законом сохранения момента импульса фотон должен иметь момент импульса целочисленно кратный постоянной ħ.

Теория Бора, несмотря на успехи в моделировании атома водорода, не помогла построить модель многоэлектронных атомов. Кроме того, она не давала объяснения и другим явлениям, например, тонкой структуре энергетических уровней.

Однако теория Бора уже не была классической теорией строения атома. Одним из важнейших результатов этой теории является демонстрация того факта, что для объяснения явлений микромира необходимы подходы, отличные от подходов классической физики.

Стационарное уравнение Шредингера для атома водорода.

Рассмотрим квантовую систему, состоящую из неподвижного ядра с зарядом Ze (Z – целое число) и электрона. Такая система при Z>1 описывает водородоподобный ион, а при Z=1 – атом водорода. Считая энергию системы постоянной, запишем уравнение Шрёдингера для стационарного состояния:

.

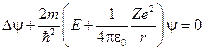Запишем это уравнение в сферической системе координат,

, , .

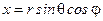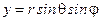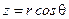Запишем оператор Лапласа в сферической системе координат:

,

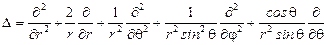тогда уравнение Шрёдингера принимает вид:

.

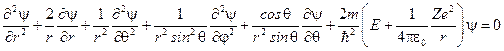Перепишем уравнение в виде

.

Для дальнейшего анализа удобно ввести обозначение угловой части оператора Лапласа:

.

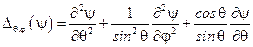Для поиска собственных функций этого оператора необходимо решить уравнение:

.

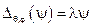Исследование этого уравнения показывает, что оно обладает непрерывным решением, если собственные числа имеют специальный вид: 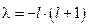, где 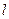- целое неотрицательное число: .

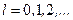Введём оператор квадрата момента импульса .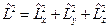

В сферической системе координат этот оператор принимает вид:

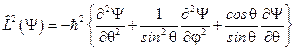или .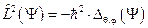

Поиск собственных значений этого оператора: 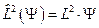приводит к уже известному уравнению: 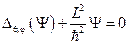, откуда следует равенство: 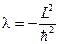или 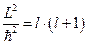для неотрицательных целых чисел l. Поэтому величина момента импульса для электрона в атоме принимает значения:

.

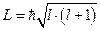Т.к. проекция вектора на ось Z не может быть больше длины вектора, то из соотношения 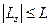и равенств 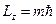, 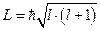получаем: 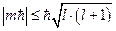или 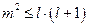. С учётом того, что числа m и l - целые, это соотношение эквивалентно тому, что значения m находятся в диапазоне: .

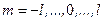Исходное уравнение Шрёдингера: 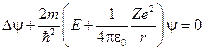, в сферической системе координат:

,

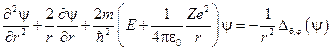а с учётом выражения для квадрата момента импульса 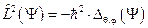может быть записано в форме, учитывающей квадрат момента импульса

.

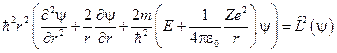Следовательно, решение этого уравнения должно зависеть от величины момента импульса.

Это уравнение имеет непрерывные решения при любых положительных значениях энергии 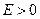. Этому случаю соответствуют решения, описывающие электрон, пролетающий мимо ядра.

Для отрицательных значений энергии 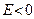непрерывные решения существуют для значений Е в уже знакомом нам виде:

,

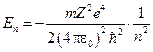где 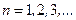. В этом случае электрон связан с ядром. При этом число l меняется в диапазоне .

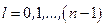Замечание. Выражение для энергии совпадает с выражением, полученным в теории атома Бора.

В итоге, можно сказать, что решение уравнения Шрёдингера для электрона в водородоподобном атоме определяется тремя целыми числами: n, l, m, что условно обозначают следующим образом: .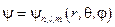

Число nопределяет значение энергии электрона в атоме и называется главным квантовым числом.

Число l определяет величину момента импульса электрона, поэтому его называют орбитальным (азимутальным) квантовым числом. Оно принимает значения из диапазона .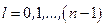

Число m называется магнитным квантовым числом. Оно определяет проекцию момента импульса на ось вращения. Принимает значения из диапазона: .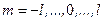

Следовательно, одному значению энергии, задаваемому главным квантовым числом n может соответствовать несколько разных функций .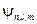

Для заданного значения l число возможных значений m равно 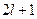. Но для заданного числа n число возможных значений l равно n. Поэтому общее количество наборов троек чисел 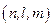равно: 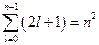. Т.е. кратность вырождения уровня энергии для главного квантового числа n равна n ². Проиллюстрируем это заключение таблицей:

n
y n , l, m		, ,	, , , , ,, , ,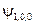
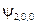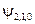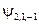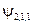
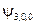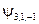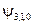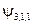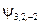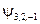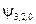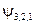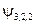
Кратность вырождения

Для обозначения квантовых состояний вводятся спектроскопические символы:

Значение числа l
Обозначение состояния	s	p	d	f	g	h

Например, электрон, находящийся в состоянии с 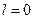, называют s -электроном, а само состояние – s -состоянием.

Значение главного квантового числа указывают перед спектроскопическим символом.

Например, символ 3 p обозначает состояние, в котором n =3, l =1. Символ 2 s обозначает состояние, в котором, n =2, l =0, и т.д.

В теории Бора изменение состояния электрона соответствует его переходу с одной орбиты на другую. В квантовой механике изменение состояния атома не связано с пространственным перемещением электрона, т.к. понятие орбиты движения электрона становится неприменимым. Например, s -состояние электрона в классической механике является невозможным, ибо в этом случае орбитальный момент импульса электрона равен нулю – т.е. электрон при своём движении с классической точки зрения проходит через ядро.

Правило отбора.

Испускание и поглощение света происходит при переходе атомов из одного состояния в другое. При этом осуществляются такие переходы, у которых изменение главного квантового числа может быть любым, но орбитальное квантовое число меняется только на единицу: 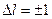. Это, например, переходы 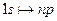или 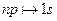. Это вызвано тем, что фотон обладает собственным моментом импульса, почти равным ħ.

Магнитное квантовое число при таких переходах меняется, не больше, чем на единицу: .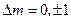

Переходы, которые удовлетворяют правилам отбора, называются разрешёнными, вероятность остальных переходов значительно меньше, они трудны для наблюдения и считаются запрещёнными.

Состояние 1 s – основное. В этом состоянии атом имеет минимальную энергию. Чтобы перевести атом в одно из возбуждённых состояний, ему надо сообщить энергию. Это можно осуществить за счёт теплового удара (соударения с другим атомом в нагретом газе), за счёт электронного удара (например, в электрическом разряде) или за счёт поглощения атомом фотона. Характерное время жизни атома в возбуждённом состоянии составляет 10^-8 с. Затем происходит спонтанный переход в состояние с меньшей энергией. Этот переход атома будет сопровождаться излучением кванта с энергией6

h ν = E _НАЧ – E _КОН,

где E _НАЧ и E _КОН - энергии соответствующих состояний.

Примеры возможных переходов для атома водорода показаны стрелками на схеме уровней.

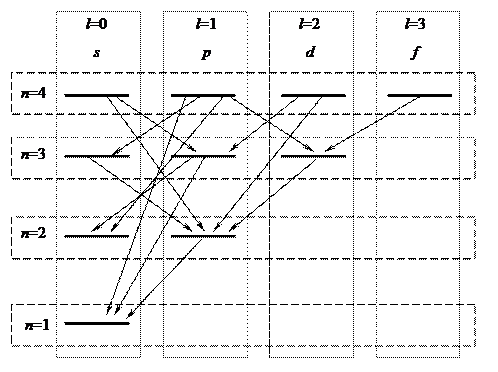
Переходы, приводящие к появлению серии Лаймана, можно записать в виде 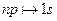(n = 2, 3,...).

Серия Бальмера – это переходы на уровень n =2: 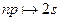, , 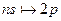, 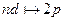(n = 3, 4,...).

Серия Пашена (серия Ритца-Пашена) – это переходы на уровень n =3 и т.д.

В атоме водорода есть состояние, переход из которого запрещён правилами отбора. На схеме уровней видно, что это 2 s - состояние. Атом в таком состоянии называют метастабильным. Время жизни может быть очень продолжительным. Возбуждённый атом водорода в метастабильном состоянии 2 s существует ~ 2 мс. Благодаря значительному времени жизни метастабильные атомы могут накапливаться до относительно высоких концентраций: 10¹² - 10¹⁴ см^-3, оставаясь возбуждёнными. Снятие возбуждений в таких системах происходит вследствие межатомных столкновений и может затягиваться на макроскопические времена.

Модель водородоподобного атома удовлетворительно описывает атомы, находящиеся на высоких уровнях энергии возбуждения.

Высоковозбуждёные атомы, (когда n >> 1), называют ридберговскими. Для атомов всех элементов высоковозбуждённые состояния водородоподобны. Причина в том, что при n >> 1 внешний электрон почти всё время удалён от иона на очёнь большие расстояния. Тем самым он движется в поле положительно заряженного атомного остатка (как в водородном атоме вокруг ядра). Отклонения от этой модели заметны только на близких расстояниях от центра. Главная особенность ридберговских состояний – универсальный для всех атомов характер, т.е. все подобные атомы по свойствам схожи. Время жизни этих состояний растет пропорционально 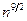и может достигать миллисекундных значений и более в зависимости от того, насколько велико главное квантовое число n.

Оказывается, что газ возбуждённых атомов конденсируется, т.к. конденсированное возбуждённое состояние энергетически более выгодно по сравнению с газовым состоянием (как в металле: электрон не принадлежит отдельному атому).

Дата добавления: 2014-01-05