Внецентренное растяжение и сжатие

При внецентренном растяжении равнодействующая внешних сил не совпадает с осью бруса, как при растяжении и смещена относительно оси и параллельна ей.

Пусть в точке 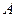приложена равнодействующая сила равная 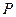. Координаты ее и 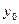. От этой силы в произвольном сечении стержня возникает нормальная сила и два изгибающих момента и (рис. 5.15).

Рис. 5.15

Причем .

Правило знаков: нормальную силу считают положительной, если она вызывает растяжение. Изгибающие моменты и считают положительными, если они вызывают растяжение в первой четверти.

Возьмем произвольную точку 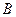с координатам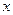и и 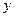. Нормальные напряжения в этой точке определяем по формуле

(5.17)

Пространственная эпюра напряжений образует плоскость. Так как эпюра напряжений образует плоскость, то положение нулевой линии определится как линия пересечения этой плоскости с плоскостью поперечного сечения. Уравнение нейтральной линии получаем, приравнивая 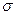нулю:

(5.18)

Расчет на прочность ведется для наиболее удаленной точки .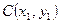

(5.19)

Эта линия не проходит через начало координат, как в случае косого изгиба. Проведем нейтральную линию, определив отрезки, отсекаемые ею на осях. Обозначим отрезки на осях отсекаемые нейтральной линией (рис.5.16,а).

Рис. 5.16

При 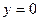, 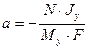— отрезок отсекаемой нулевой линии на ос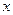и . При , 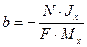— отрезок отсекаемой нулевой линии на оси 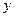. Заменим 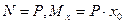, тогда .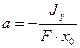

Введем понятие радиуса инерции

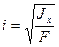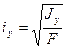(см), (см)

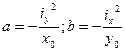. Если 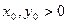, то .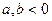

Если точка приложения силы 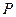приближается к центру, то нулевая линия будет уходить в бесконечность и наоборот. Если нейтральная линия пересекает поперечное сечение (рис. 5.16,а), то в частях, расположенных по разные стороны от нее, нормальные напряжения (5.16) имеют разные знаки. Пусть нейтральная линия касается контура поперечного сечения (положение ). Соответствующая точка приложения силы находится в полюсе . 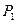Если теперь катить нейтральную линию по контуру сечения (положение 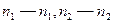и т.д.), то полюс 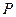будет описывать вокруг центра тяжести сечения 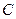некоторую замкнутую кривую (рис. 5.16,б), область внутри которой называется ядром сечения. Если сила приложения внутри ядра сечения, то нейтральная линия находится вне сечения и в нем возникают напряжения одного знака.

Глава 6. ПЕРЕМЕЩЕНИЯ ПРИ ИЗГИБЕ

Дата добавления: 2014-01-05