Метод сил. Выбор основной системы

Классификация стержневых систем. Системы статической неопределимости

Введение

Под стержневой системой в общем случае понимается любая конструкция, состоящая из элементов имеющих форму бруса. Стержневые системы принято разделять на статически определимые и статически неопределимые. В статически определимых системах все усилия определяются только с помощью уравнений равновесия. В статически неопределимых системах для определения усилий уравнений статики недостаточно.

Стержневые системы можно разделить на три группы: плоские; плоскопространственные; пространственные. Рассмотрим только плоские системы. В них все стержни и внешние силы лежат в одной плоскости. К ним относятся: фермы, балки, рамы (рис. 7.1).

Рис. 7.1

Ферма (рис.7.1, а) — стержневая конструкция, элементы которой работают преимущественно на продольную силу. Нагрузка прикладывается в узлах фермы. Балка — прямой брус, работающий на изгиб (рис. 7.1, б). Рама — стержневая система, элементы которой работают преимущественно на изгиб (рис. 7.1, в).

Степень статической неопределимости — число “лишних связей”, удаление которых делают систему статически определимой и геометрически (кинематически) неизменяемой. Геометрически неизменяемой называют систему, изменение формы которой происходит только в связи с деформацией ее элементов.

Известно, что положение бруса в пространстве определяется шестью независимыми координатами, т.е. брус обладает шестью степенями свободы.

На брус могут быть наложены связи, фиксирующие его положение на плоскости (рис.7.2). Если на левый конец балки наложено условие, запрещающее вертикальные перемещения (рис. 7.2, а), то в этой точке имеется одна внешняя связь. Если запрещено как вертикальное, так и горизонтальное, то наложены две связи (рис. 7.2, б). Заделка полностью фиксирует положение стержня в плоскости (рис. 7.2, в).

Рис. 7.2

Примеры определения степени статической неопределимости.

Ферма (рис.7.1,а)

,

где — степень статической неопределимости;

— число стержней, включая и опорные;

— число узлов фермы.

. Следовательно, данная ферма один раз статически неопределимая.

Балка (рис. 7.1, б)

,

где — число опорных реакций, тогда , т.е. данная балка два раза статически неопределимая.

Рама (рис. 7.1,в)

,

где 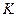— число замкнутых контуров;

— число врезанных шарниров.

Первая рама внешним образом статически неопределимая, для нее . Вторая рама имеет замкнутый контур и врезанный шарнир, для нее .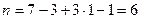

Одним из наиболее распространенных методов расчета статически неопределимых систем (С.Н.С.) является метод сил. Он заключается в том, что заданная С.Н.С. освобождается от «лишних» связей, а их действие заменяются неизвестными силами и моментами. Величина их подбирается так, чтобы перемещения в основной (эквивалентной) системе были равны перемещениям в заданной системе. Основной называется статически определимая, геометрически (кинематически) неизменяемая система, полученная из заданной путем отбрасывания лишних связей и заданных нагрузок. Как правило, для одной статически неопределимой системы можно подобрать сколько угодно основных систем.

Рассмотрим плоскую раму (рис. 7.3). Степень статической неопределенности «» равно . Выберем несколько вариантов основных систем, отбрасывая каждый раз семь «лишних» связей. Например, для данной рамы можно предложить основные системы а), б), ………., которые получены путем отбрасывания семи связей в различных комбинациях.

Рис. 7.3

Эквивалентная система — получается из основной, путем загружения неизвестными реакциями отброшенных связей, а также заданной внешней нагрузкой (рис. 7.4).

Рис. 7.4

Там, где запрещены линейные перемещения, приложены силы, где угловые — моменты, где взаимные — взаимные моменты и силы.

Теперь остается составить уравнения для определения неизвестных .

Дата добавления: 2014-01-05