Способ Верещагина

Основным недостатком при определении перемещений с помощью интегралов Мора является необходимость составлять аналитические выражения подынтегральных функций и дальнейшего их интегрирования. Это особенно неудобно при большом количестве участков, т.к. приводит к громоздким вычислениям.

Если брус состоит из прямых участков с постоянной, в пределах каждого участка жесткостью, то операцию вычисления интегралов Мора можно упростить. Это упрощение основано на том, что эпюры от единичных силовых факторов на прямолинейных участках бруса всегда будут линейными.

Пусть на участке длиной 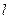нужно взять интеграл от произведения двух функций

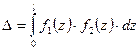(6.9)

при условии, что по крайне мере одна из функций — линейная. Пусть 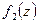— линейная, тогда 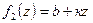(рис.6.5).

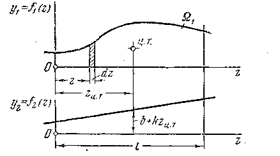
Рис. 6.5

Тогда выражение (6.9) примет вид 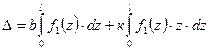. Первый из интегралов представляет собой площадь ограниченную кривой 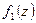, т.е. площадь криволинейной эпюры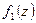

.

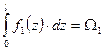Второй интеграл представляет собой статический момент этой площади 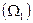относительно 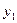, т.е.

,

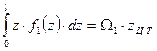где 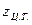— координата центра тяжести первой эпюры.

В результате получим

.

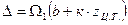Но .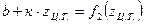

Следовательно 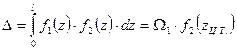. (6.10)

Таким образом, по способу Верещагина операция интегралов заменяется перемножением площади первой эпюры на ординату второй (линейной) эпюры взятую под центром тяжести первой. Если обе функции линейные, то операция перемножения обладает свойством коммутативности.

На первый взгляд способ Верещагина не дает существенных упрощений, т.к. его применение требует построения эпюр внутренних усилий от заданной и единичных сил и перемножения их. Однако почти все встречающиеся на практике эпюры внутренних усилий могут быть, как правило, разбиты на три простейшие фигуры: прямоугольник, треугольник и параболу (рис. 6.6).

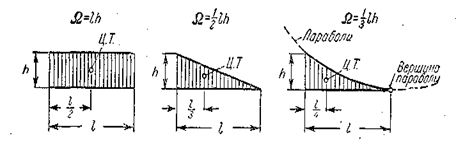
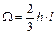
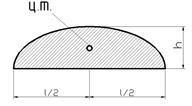
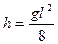
Рис. 6.6

Глава 7. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СТЕРЖНЕВЫЕ СИСТЕМЫ

Дата добавления: 2014-01-05