Совершенствование алгоритмов обработки экспериментальных данных

Развитие теории и совершенствование АОЭИ определяются корректным решением с высокой достоверностью и заданной точностью задачи оценивания этих данных [36]. Оценивание обеспечивает наилучшее восстановление полезной информации по экспериментальным данным, которые получены в условиях помех. Для стохастического контроля типичная схема измерения Гаусса – Маркова в физическом эксперименте отвечает стандартной системе “объект – среда – прибор” [6, 54, 59, 77], в которой результат измерения дается в виде равенства

y = Ax + v, (1.1)

где v – шумы, сопровождающие процесс измерения; А – интегральный оператор с ядром k (t).

Решение задачи оценивания для такой схемы измерения с помощью АОЭИ, структура которого приведена на рис. 1.1 в виде ИИУ, заключается в извлечении из выходного параметра y, полученного в результате эксперимента, как можно более точных значений параметров объекта, причем не искаженных в процессе измерения, а других – свойственных системе “объект – среда”, не возмущенных измерениями. При этом оценка контролируемого параметра для стохастического эксперимента определяется в виде математического ожидания.

Если передаточная функция W (s) первичного преобразователя (ПП) с входным x и выходным z параметрами в комплексной области имеет вид

W (s) = Z (s)/ X (s), (1.2)

где Z (s) =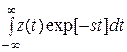, X (s) =, то в действительной области она представляется интегральным уравнением Фредгольма, которое может быть преобразовано к интегральному уравнению Вольтерра первого рода [103]

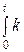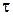z (t) = (t) х (t – t) d t = ) x () d 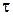= Аx, (1.3)

где k (t) – ядро интегрального уравнения (импульсная функция ПП от передаточной функции (1.2)).

Обычно, в соответствии с уравнением (1.1), входная информация x поступает одновременно от объекта и среды, которые взаимодействуют между собой и с ПП, поэтому в результате измерения в “чистом виде“ параметры объекта не могут быть получены. Неявно они содержатся во входном параметре x, но непосредственно не наблюдаемы, т. е. x ÎW _x – случайный процесс, непосредственное наблюдение которого невозможно. Для определения x наблюдают за параметром у, функционально связанным с параметром x. В выходном параметре y ПП (рис. 1.1) характеристики объекта присутствуют в искаженном виде, обусловленном свойствами ПП и соответственно оператора А, и разрушающим действием шума v, сопровождающего измерение [54, 1, 79]. В результате для реального ПП имеем

z (t; a, b) = М{ Y (t)| х (s); s Î Т } = 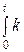(t; a, b) х (t – t) dt = Аx, (1.4)

где а – параметр ПП, зависящий от внешней среды; b – вектор “паразитных” параметров, сопровождающих измерения.

В общем виде реальное ИИУ может быть многомерным, нестационарным и в нем могут не выполняться другие ограничения, связанные с представлением его при помощи линейного интегрального оператора. Однако некоторые физические и технологические сведения о ИИУ позволяют принять в качестве первого приближения случайные функции входа и выхода модели стационарными или стационарно связанными в широком смысле, а модель (1.3, 1.4) – линейной, при условии проверки степени идентичности принятой модели реальному ИИУ, которая определяется по фактическим реализациям y (t) и x (t).

Математическое описание ИИУ при помощи модели (1.4) имеет следующую интерпретацию: из множества факторов, действующих в реальном объекте на выходную переменную y (t), учитывается только одна входная переменная x (t). Эта связь представляется в виде (1.4), причем для рассматриваемой на рис. 1.1 схемы измерения данное интегральное уравнение имеет погрешность в правой части, то есть z (t) оценивается с погрешностью измерения, которая определяется величиной шумов процесса измерения v. На выходе ИИУ формируются редуцированные (эффективные) величины [112], которые характеризуют параметр измерения по его воздействию на ПП.

Решение уравнения (1.4) сводится к интегральному уравнению Вольтерра, ядро которого равно резольвенте исходного интегрального уравнения [103], т.е. решение задачи оценивания параметра объекта является также редуцированной величиной и должно уменьшать искажения при измерении, приближая их к значениям, свойственным объекту, а его результат естественно назвать редукцией результатов измерения к параметру объекта. Причем в процессе измерения с погрешностью определяются и пределы интегрирования t, а ядро данного интегрального уравнения (импульсная функция ПП) k (t; a, b) тоже может идентифицироваться с определенной точностью, поскольку параметр ПП, входящего в ИИУ дестабилизирует среда, в которой производится измерение. Таким образом, рассматриваемая задача редукции уравнения (1.4) относится к классу некорректных задач. При этом обобщенная задача оценивания параметров объекта по результатам измерения сводится к решению идентификационно – редукционной задачи, а выбор и обоснование алгоритма решения данной задачи являются узловыми вопросами оценки параметров измерения и требуют специальных исследований. Особенность алгоритмизации идентификационно – редукционной задачи выделяет новый класс алгоритмов – идентификационно – редукционных. Предметная область данного исследования находится на стыке теории измерения и алгоритмики, образующих интенсивно развивающййся раздел теории измерения – операционализм [115], в рамках которого осуществляется синтез алгоритмов и исследование вопросов их сходимости и эффективности.

Дата добавления: 2014-01-05