Информационная мера степени изоморфности модели

Полученный общий показатель качества ММИ может быть использован для целенаправленного ее поиска в соответствии с работами [76, 84]. В качестве характеристики состоятельности выбора элемента модели заданного ПП по экспериментальным данным в выражении (2.1) используется понятие надежности как вероятности ошибочно отвергнуть модель на основании экспериментальных данных y. При этом модель М рассматривается как параметр распределения y и решается задача проверки гипотезы М = М₀ против любой из альтернатив М Î М, где М₀ – модель, используемая для интерпретации результатов измерения y, М – класс альтернативных моделей. Качество АОЭИ определяется надежностью выбора ММИ, то есть изоморфностью модели результатам эксперимента, и надежностью самой операции редукции измерения, которые определяются соответствующими рисками.

Для введения меры, характеризующей степень изоморфности выбранной ММИ, воспользуемся основными положениями теории информации [66]. Риск, характеризующий принятую модель М₀ Î М, определяется, в том числе, уровнем неопределенности в предсказании результата, к которому может привести выбранная модель М₀ при оценке состояния объекта. Задача выбора элемента модели ПП относится к классу задач по распознаванию образов, т.е. концептуально выбор элемента ММИ сводится к распознаванию состояния X_i объекта (образа) и выбор конкретного решения на основании распознанного состояния X_i по заданной классификации стандартных моделей М. Таким образом, рассматриваемая задача принятия решения относится к классу задач обучения распознаванию образов.

В задаче выбора элемента модели функция потерь равна нулю (принята правильная модель) либо величине ошибочно принятой оценки модели (принята неправильная модель). Эта особенность задачи минимизации риска выбора элемента модели и определяет специфику данного класса задач. Определённый таким образом риск для задачи классификации позволяет, исходя из общего определения риска, приведенного в разд. 1.2, представить риск выбора элемента модели в следующем виде [80]:

R _М(a) = R ₀= R ₀ R ₁,

где R ₀ – квадрат принятой оценки модели; R ₁ – приведенный риск.

Для конкретизации введенного в соответствии с данным выражением понятия приведенного риска выбора элемента модели, рассмотрим функцию S (x ₀) = P (х > х ₀), определяющую вероятность преодоления уровня х ₀ [87]. Если F (х) функция распределения случайной величины Х, то

S (х ₀) = 1 – F (х ₀). (2.8)

Если функция распределения F (х) абсолютно непрерывна, то обозначим через f (х) соответствующую плотность распределения случайной величины. Интенсивностью риска по элементам с распределением F (x) назовем функцию 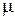(х, x ₀), характеризующую совместную плотность вероятности параметра x при условии его выхода за заданный предел x ₀, которая определяется выражением (в соответствии с теоремой Байеса):

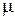(х, x ₀) = [ f (x)× f _2|1(x > x ₀| x)]/[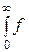(x)× f _2|1(x > x ₀| x) dx ],

где f _2|1(x > x ₀| x) – представляет собой функцию-индикатор множества x > x ₀. В связи с чем

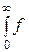(x)× f _2|1(x > x ₀| x) dx = f _2|1(x > x ₀| x)(x) dx

и, следовательно,

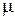(х, x ₀) == 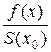. (2.9)

При этом для функции S (x ₀) из уравнения (2.9), с учетом выражения (2.8), следует

S (х ₀) = exp[–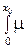(х, x ₀) dx ]. (2.10)

Интенсивность риска характеризует вероятность выхода переменной за предел х ₀ на малом интервале [ x ₀, x ₀ + 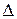x), при условии его достижения значения х ₀ P (x ₀ 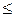x < x ₀ + 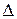x | x > x ₀) = =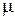(x ₀)× 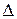x + o (x).

Определение. Под интегральной интенсивностью риска при выборе по экспериментальным данным элемента ММИ М ₀Î М, с заданной областью ее значений D ₀, понимается условная вероятность P (x Î D ₁| D ₀) попадания выходных параметров выбранной модели М ₀ в диапазон D ₁¹ D ₀.

Таким образом, интегральная интенсивность риска выбора элемента модели характеризуется, при выбранной оценке модели, вероятностью P (x Î D ₁| D ₀) при условии, что объект находится в заданном исходном диапазоне D ₀ (условная вероятность), и диапазоном D ₁, в который может попасть выходной параметр модели. Интегральная интенсивность риска определяет вероятность неправильной идентификации параметра x по экспериментальным данным и равна вероятности ошибки первого рода [114].

Продифференцировав равенство (2.10) по x ₀, получаем

dS (x ₀)/ dx ₀=–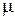(x ₀)×exp[–(х, x ₀) dx ].

После несложных преобразований имеем [ln f (x ₀) – ln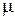(x ₀)] = (x, x ₀) dх.

Усреднив интегральную интенсивность риска на интервале [0, х ₀) по распределению f (х), получаем выражение для приведенного риска:

R ₁^*(x 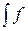₀) =(х ₀)(x, x ₀) dхdх ₀ = 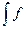(х ₀)×ln dх ₀. (2.11)

Таким образом, усредненный приведенный риск на заданном интервале усреднения [0, х) совпадает с выражением для энтропии Кульбака–Лейблера [66], то есть равен “функции различения” между статическим распределением f (x) и интегральной интенсивностью риска 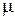(x), которая равна плотности вероятности выхода переменной x за заданный предел x ₀, что совпадает и с интуитивным пониманием риска. Подобно можно определить риск каждого элемента модели и ее отношений, что в итоге позволяет определить риск общей модели по выражению (2.1). Полученная информационная мера изоморфности (2.11) может быть обобщена для статических многомерных и динамических моделей. При этом входными переменными модели является векторная случайная величина X (Х ₁,..., Х_i,..., Х_n), а выходными – векторная случайная величина Y (Y ₁,..., Y_j,..., Y_m). Тогда риск j -й выходной переменной будет равен

R _M{ Х ₁,..., Х_n; Y }= R ₀(х ₁,..., х_n; у_j)log 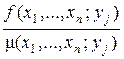dхdу.

Согласно определению, величина R _M(Х ₁,..., Х_n, Y_j } характеризует неопределенность выходной величине АОЭИ, которая определяется по вектору входных величин при рассмотрении их совместного влияния на параметр Y_j. Данное выражение согласуется с выражением (2.7), которое определяет надежность композиционной модели.

Дата добавления: 2014-01-05